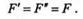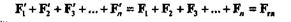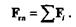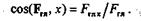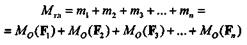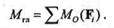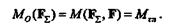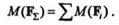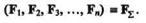Лемма о параллельном переносе силы

Лемма.Механическое состояние твердого тела не нарушится, если данную силу перенести параллельно первоначальному положению в про-

36

 

извольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

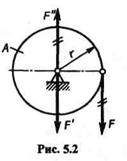
Возьмем тело, находящееся под действием некоторой системы сил, в числе которых есть сила F, приложенная в точке А (рис. 5.1). Выберем произвольную точку О,которую назовем центром приведения, и на основании аксиомы IV приложим в этой точке две равные силы F' и F", параллельные данной силе F, причем

 

Систему сил (F, F', F"), эквивалентную силе F, представим как силу F, перенесенную параллельно первоначальному положению в произволь­но выбранный центр приведения О,и пару (F, F"), момент которой равен моменту данной силы относительно центра приведения О,являющегося новой точкой приложения силы:

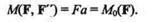
Лемма доказана.

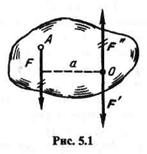
Описанный выше перенос силы можно показать на примере. Рас­смотрим колесо А радиуса г, вращающееся на оси в подшипниках (рис. 5.2). Пусть к ободу колеса по касательной приложена сила F (такую силу на­зывают окружной).

Для определения действия силы F на колесо и подшипники приме­ним доказанную лемму и перенесем эту силу параллельно самой себе на ось колеса. В результате получим силу F' = F, вызывающую давление на подшипники, и пару сил (F, F") с моментом, равным Fr, которая будет вращать колесо.

Приведение плоской системы

Произвольно расположенных сил к данному центру

Приведением системы сил называется замена ее другой систе­мой, эквивалентной первой, но более простой.

37

Теорема.Плоская сис­тема произвольно располо­женных сил в общем случае эквивалентна одной силе, приложенной в центре при­ведения, и одной паре.

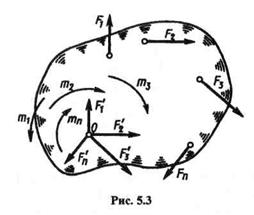
Пусть дана плоская сис­тема п произвольно распо­ложенных сил (F₁, F₂, F₃, ..., F_п-1, F_п). Перенесем парал­лельно все силы в произволь­но выбранный в плоскости действия сил центр приведе­ния О, добавив при этом п пар (рис. 5.3). Моменты этих пар т₁, т₂, т₃, ..., т_п,равны моментам данных сил относительно центра приведения О.

Вместо заданной системы п произвольно расположенных сил мы по­лучили систему и сил, приложенных в центре приведения, равных дан­ным силам по модулю и одинаковых с ними по направлению, и систему п присоединенных пар:

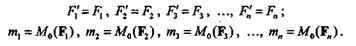
Эта новая система эквивалентна данной.

Плоская система сил, приложенных в одной точке, эквивалентна од­ной силе, которая равна векторной сумме этих сил и приложена в той же точке, следовательно,

или

Эту силу назовем главным вектором данной системы. Глав­ный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.

Графически главный вектор выражается замыкающей стороной си­лового многоугольника, построенного на данных силах. Аналитически модуль главного вектора можно вычислить по формуле

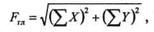
а направляющий косинус — по формуле

38

 

Плоская система пар эквивалентна одной паре, момент которой ра­вен алгебраической сумме моментов данных пар, следовательно,

или

Эту пару с моментом М_глназовем главным моментом задан­ной системы сил.

Главный момент плоской системы произвольно расположенных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.

Таким образом, всякая плоская система сил в общем случае эквива­лентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.

Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенное для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или невозможно, а глав­ный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающим­ся валом и подшипником скольжения, как правило, неизвестны, но глав­ный момент этих сил можно определить простым измерением; второй пример: в характеристику электродвигателя входит не сила, с которой статор действует на ротор, а вращающий момент.

 

Свойства главного вектора

И главного момента

      

   Свойства главного вектора и главного момента заключаются в сле­дующем:

1) модуль и направление главного вектора данной системы не зави­сят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же;

2) величина и знак главного момента в общем случае зависят от вы­бора центра приведения (кроме одного случая, о котором будет сказано в § 5.4), так как при перемене центра приведения меняются плечи сил, а модули их остаются неизменными;

39

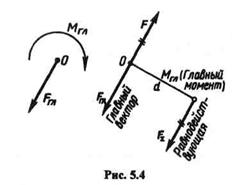
        3) главный вектор и равно­действующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть извест­ны главный вектор F_гл и глав­ный момент М_гл какой-то пло­ской системы сил (рис.5.4).Оп­ределим равнодействующую этой системы.

Пользуясь известным свой­ством пары сил, преобразуем главный момент М_глтак, чтобы

 

 силы пары F и F 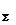- были параллельны и по модулю равны главному век­тору F _гл:

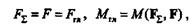
причем сила F приложена к точке О противоположно F _гл.

Далее систему (F _гл, F), как взаимно уравновешенную, отбросим:

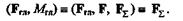
В результате получили одну силу F 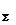 эквивалентную главному век­тору и главному моменту, т. е. равнодействующую системы, причем

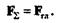
Модуль равнодействующей

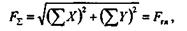
а положение линии действия равнодействующей определяется плечом d по формуле

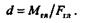
В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквивалентны;

4) главный вектор и равнодействующая эквивалентны лишь в част­ном случае, когда главный момент системы равен нулю; последнее воз­можно в случае, когда центр приведения находится на линии действия равнодействующей.

Из рис 5.4 видно, что момент равнодействующей F 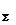- относительно

центра приведения О равен моменту М_гл  пары (F 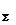, F), т. е. главному мо­менту данной системы:

40

 

Так как М_гл = 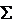M₀(F_i), а за центр приведения можно взять любую точку плоскости действия сил данной системы, то всегда имеем

 

Полученная формула является математическим выражением теоремы о моменте равнодействующей.

Теорема.Момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраиче­ской сумме моментов составляющих сил относительно той же точки.

Теорему о моменте равнодействующей впервые доказал француз­ский ученый Вариньон (1654—1722), поэтому ее называют теоремой Вариньона.

Применим доказанную теорему для определения положения линии действия равнодействующей F 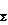 плоской системы п параллельных сил:

 

Выберем какую-либо точку О плоскости действия сил за центр мо­ментов и согласно теореме Вариньона запишем

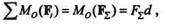
где d —плечо равнодействующей F 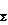 относительно точки О.

Из последнего равенства определяем плечо d:

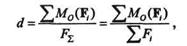
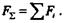так как, согласно § 3.2,

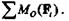Чтобы установить, в какую сторону от точки О следует на перпенди­куляре к линиям действия сил отложить плечо d, следует учесть, во-первых, направление вектора F  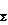и, во-вторых, знак 

                                                               

Различные случаи приведения

---

Дата добавления: 2018-04-15; просмотров: 909; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!