Проекции силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методике проекций.

Проекцией силы на ось называется отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
Пусть даны координатные оси х, у,сила Р, приложенная в точке А и расположенная в плоскости координатных осей (рис. 2.3).
Проекциями силы Р на оси будут отрезки аb и а'b'.Обозначим эти проекции соответственно Рх и Ру. Тогда
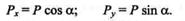
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции. За направление проекции примем направление от проекции начала к проекции конца вектора силы.
Установим следующее правило знаков:
если направление проекции силы на ось совпадает с положительным направлением оси, то эта проекция считается положительной, и наоборот.
Если вектор силы параллелен оси,то он проецируется на эту ось в натуральную величину (рис. 2.3, сила F).
Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю (рис. 2.3, сила Q).
Зная две проекции Рх и Ру,из треугольника ABC определяем модуль и направление вектора силы Р по следующим формулам:
модуль силы
|
|
| направляющий тангенс угла между вектором силы Р и осью х |
|
|
Отметим, что силу Р можно представить как равнодействующую двух составляющих сил Рх и Py,параллельных осям координат (рис. 2.3). Составляющие Рх и Py,и проекции Рх и Py, принципиально отличны друг от друга, так как составляющая есть величина векторная, а проекция — величина алгебраическая; но проекции силы на две взаимно перпендикулярные оси х и у и модули составляющих той же силы соответственно численно равны, когда сила раскладывается по двум взаимно перпендикулярным направлениям, параллельным осям х и у.
Аналитический способ определения равнодействующей плоской системы сходящихся сил
Пусть дана плоская система п сходящихся сил
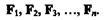
Равнодействующая этой системы
|
|
В плоскости действия данной системы выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось.
Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е.

Правую часть этого равенства записываем упрощенно, а именно:

Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат х и у, алгебраически сложим проекции всех сил и найдем, таким образом, проекции равнодействующей:
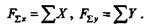
Зная проекции, на основании формул, полученных в § 2.3, определим модуль и направление равнодействующей: модуль равнодействующей
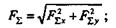
направляющий тангенс угла между вектором F  и осью х
и осью х

24
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Дата добавления: 2018-04-15; просмотров: 5924; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



