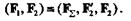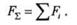ПЛОСКАЯ СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ
И МОМЕНТ СИЛЫ
Сложение двух параллельных сил,
Направленных в одну сторону
Система сил, линии действия которых параллельны и лежат в одной плоскости, называется плоской системой параллельных сил.
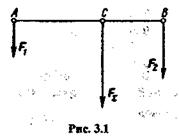
Из физики известно (рис. 3.1), что: две параллельные силы, направленные в одну сторону, эквивалентны равнодействующей, которая равна сумме этих сил, параллельна им и направлена в ту же сторону; линия действия равнодействующей делит отрезок, соединяющий точки приложения данных сил, на части, обратно пропорциональные этим силам:
26
|
|
|
|
|
|
| Применяя производную пропорцию, можно записать: |
тогда
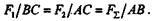
Разложение данной силы на две параллельные составляющие производится с помощью формул сложения двух параллельных сил.
Разложение силы на две параллельные составляющие есть задача неопределенная, имеющая бесчисленное множество решений. Для того чтобы задача имела определенное решение, необходимо иметь два дополнительных условия, например модуль одной составляющей и длину одного плеча, длины двух плеч и т. п.
Сложение двух неравных
Антипараллельных сил
Рассмотрим случай сложения двух не равных по модулю антипараллельных сил. Случай, когда такие силы равны по модулю, особый и рассмотрен в гл. 4.
Теорема.Две неравные антипараллельные силы эквивалентны равнодействующей, которая равна разности данных сил, параллельна им и направлена в сторону большей силы; линия действия равнодействующей делит отрезок, соединяющий точки приложения данных сил, внешним образом на части, обратно пропорциональные этим силам.
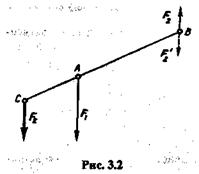
Рассмотрим две параллельные силы F1 и F2, причем F1 > F2 (рис. 3.2). Разложим силу F1 на две параллельные составляющиеF 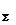 иF'2 так, чтобы
иF'2 так, чтобы
|
|
составляющая F'2 была приложена в точке В и F'2 = F2. Тогда на основании
|
|
| Из этих равенств найдем модуль второй составляющей F 27 |
теоремы о сложении двух параллельных сил, направленных в одну сторону, получим
АС до точки ее приложения (известно, что F'2 = F2).
Данная система сил (F1 ,F2) заменена системой трех сил:
|
|
Отбросив на основании аксиомы IV две взаимно уравновешенные силы F2 и F'2, получим, что данная система эквивалентна одной силе, т. е.
равнодействующей F 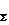 :
:
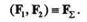
Модуль и точка приложения равнодействующей определяются по формулам
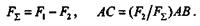
Отметим, что равнодействующая двух параллельных сил равна их алгебраической сумме.
Если на тело действует система л параллельных сил, то, производя последовательное сложение сначала двух сил, их равнодействующей с третьей силой, новой равнодействующей с четвертой силой и т. д., найдем модуль и линию действия равнодействующей всей системы параллельных сил.
Очевидно, что равнодействующая системы параллельных сил определится в результате алгебраического сложения сил данной системы:
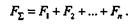
Таким образом, равнодействующая системы параллельных сил равна их алгебраической сумме:
|
|
Вопрос о положении линии действия равнодействующей легко решается с помощью теоремы, доказанной в § 5.3.
Дата добавления: 2018-04-15; просмотров: 898; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

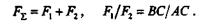
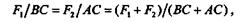
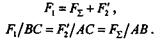
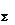 и расстояние
и расстояние