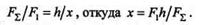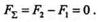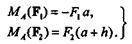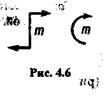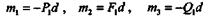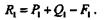Момент силы относительно точки

⇐ ПредыдущаяСтр 7 из 72Следующая ⇒

Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное дейст-

вие силы характеризуется моментом силы.

Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519).

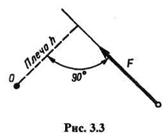
Моментом силы относительно точки называется произведение модуля силы на ее плечо (рис. 3.3):

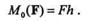
Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.

Единица момента силы:

[М] = [F] 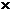[h] = сила 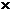длина = ньютон метр=Н м.

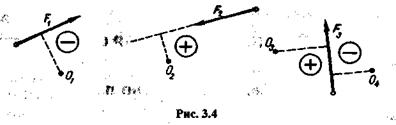
Условимся считать момент силы положительным, если сила стремится вращать свое плечо вокруг центра момента против часовой стрелки, и наоборот (рис. 3.4).

Одна и та же сила относительно разных точек может давать и положительный и отрицательный момент (рис. 3.4. сила F₃).

Момент силы относительно точки, лежащей на линии действия этой силы, равен нулю, так как в этом случае плечо равно нулю.

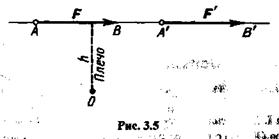
Из рис. 3.5 видно, что момент силы относительно точки не меняется при переносе силы вдоль линии ее действия, так как модуль силы и плечо остаются неизменными.

Глава 4

ПЛОСКАЯ СИСТЕМА ПАР СИЛ

Пара сил и момент пары

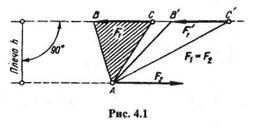
В § 3.2 нами был исключен из рассмотрения случай сложения двух антипараллельных сил, равных по модулю. Такая система сил называется парой сил или просто парой (рис. 4.1).

Понятие пары сил введено в механику в начале XIX в. французским ученым Пуансо (1777—1859), который разработал теорию пар.

Плоскость, в которой расположена пара, называется плоскостью действия пары. Расстояние между линиями действия сил есть плечо пары. Эффект действия пары состоит в том, что она стремится вращать тело, к которому приложена. Ее вращательное действие определяется моментом пары.

Моментом пары называется произведение модуля одной из сил, составляющих пару, на плечо:

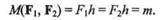
Момент пары и момент силы имеют одинаковую размерность.

Условимся считать момент пары положительным, если она стремится вращать свое плечо против часовой стрелки, и наоборот.

Момент пары численно равен удвоенной площади треугольника, у которого основанием является вектор одной из сил пары, а высотой — плечо.

Из рис. 4.1 видно, что момент пары не меняется при переносе сил вдоль линий их действия, так как треугольники ABC и АВ’С’ — равновеликие.

Основные свойства пары

Основные свойства пары характеризуются следующими тремя теоремами.

Теорема I. Пара сил не имеет равнодействующей.

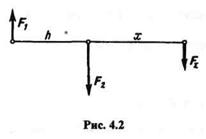
Дана пара (F₁, F₂) с плечом h (рис. 4.2).

Предположим, что F₂> F₁.Тогда равнодействующая этих сил F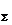= F₂ - F_l, а точка ее приложения определяется из пропорции

Пусть теперь сила F₂уменьшается и приближается по модулю к силе F₁,тогда в пределе при F₁= F₂

Это значит, что приF₁= F₂ равнодействующая не существует.

Из этой теоремыследует, чтопара сил не может быть уравновешена одной силой, пара сил может быть уравновешена только парой.

Теорема П.Алгебраическая сумма моментов сил, составляющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.

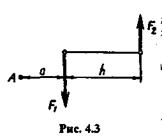
Дана пара (F₁, F₂) с плечом h (рис. 4.3) и моментом т = F₁h= F₂h.

Выберем в плоскости действия пары произвольную точку А и примем ее за центр моментов:

Сложим правые и левые части этих равенств: M_A (F₁) + M_A(F₂)= -F₁a + F₂(a + h)= F₂h,или

M_A (F₁) + M_A(F₂)= m;теорема доказана.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

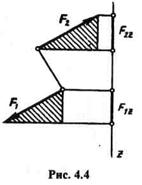
Теорема Ш.Алгебраическая сумма проекций сил пары на ось всегда равна нулю.

Дана пара (F₁, F₂) и ось z,лежащая в плоскости действия пары (рис. 4.4). Из равенства заштрихованных треугольников видно, что F₁_z = F₂_z. Проекция F₁_z — положительная, про-

екция F₂_z— отрицательная, следовательно, их алгебраическая сумма все
гда равна нулю.

Из этой теоремы следует, что пара сил не входит ни в уравнение сил, ни в уравнение проекций сил.

Эквивалентные пары

Две пары называются эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела.

Теорема об эквивалентных парахформулируется так: если моменты двух пар алгебраически равны, то эти пары эквивалентны.

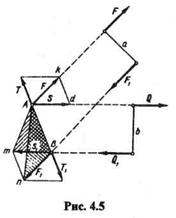
Даны две пары (F, F₁) и (Q, Q₁), моменты которых алгебраически равны (рис. 4.5), т. е.

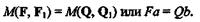
Продолжим линии действия сил пары до их взаимного пересечения в точках А и В.На основании следствия из аксиом III и IV перенесем силы F и F₁ вдоль линий их действия в точки А и В.Соединим эти точки прямой линией и разложим силы Fи F₁ по направлению АВ и вдоль линий действия сил Q и Q₁. Из равенства треугольников Akd и Втп вытекает, что Т=Т₁и S = S₁.

Силы Т и T₁ представляют собой уравновешенную систему, так как они равны по модулю и действуют по одной прямой в противоположные стороны. На основании аксиомы IV такую систему можно отбросить.

Силы S и S₁ представляют собой пару сил с плечом b.Таким образом, пара (F, F₁) 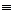паре (S, S₁).

Рассмотрим треугольники АтВ и АпВ.Они имеют общее основание

АВ, а высоты их равны, следовательно,

пл. 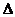АтВ - пл. 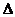АпВ.

Но удвоенная площадь 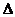АпВ численно равна моменту пары (F, F₁), а удвоенная площадь 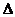АтВ численно равна моменту пары (S, S₁), следовательно, М(F,F₁) = M(S, S₁) или Fa = Sb.

По условиям теоремы Fa = Qb,следовательно, Sb = Qb,отсюда S= Q, S₁ = Q₁.

Силы S и Qравны по модулю, действуют по одной прямой в одну сторону, следовательно, они эквивалентны друг другу; на этом же основании эквивалентны

друг другу силы S₁ и Q₁. Следовательно, пара (Q, Q₁) 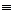паре (S, S₁).

Но выше доказано, что пара (F, F₁) 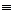паре (S, S₁).

Так как две пары порознь эквивалентны одной и той же третьей паре, то эти пары эквивалентны между собой, т. е.

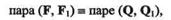
что и требовалось доказать.

Из доказанной теоремы об эквивалентных парах вытекает четыре следствия:

1) не изменяя механического состояния тела, пару можно перемещать как угодно в плоскости ее действия;

2) не изменяя механического состояния тела, можно менять силы и плечо пары, но так, чтобы ее момент оставался неизменным;

3) чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент» и условно изображают его так, как показано на рис. 4.6;

4) условия равновесия плоской системы параллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары параллельно другим силам системы.

Теорема о сложении пар

Теорема.Всякая плоская система пар эквивалентна одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.

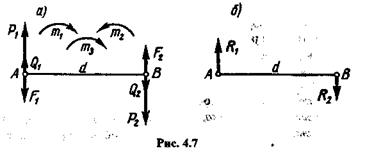
Пусть даны три пары с моментами т₁, т₂, m₃, действующие в одной плоскости (рис. 4.7, а).

На основании следствия из теоремы об эквивалентных парах преобразуем эти пары так, чтобы их плечи стали равными d,и перенесем к произвольно взятому на плоскости отрезку АВ длиной d.

Тогда вместо заданной системы пар получим новую систему, эквивалентную данной, причем моменты данных и новых пар будут равны, т. е.

Сложив три силы в точке А,получим равнодействующую R₁ (рис. 4.1, б), модуль которой

Сложив три силы в точке В,получим равнодействующую R₂, модуль которой

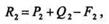
причем очевидно, что силы R₁ и R₂ равны по модулю, параллельны и противоположно направлены.

Значит, система (R₁, R₂) представляет собой пару с плечом d, эквивалентную данной системе пар.

Момент этой результирующей пары

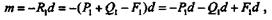
или

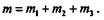
Аналогичное доказательство можно привести для любой плоской системы пар, т. е. в общем виде можно записать

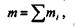
что и требовалось доказать.

Дата добавления: 2018-04-15; просмотров: 1149; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!