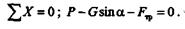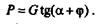Трение на наклонной плоскости

Рассмотрим тело, лежащее на шероховатой наклонной плоскости, составляющей угол а с горизонтальной плоскостью (рис. 6.5). Разложим силу G на составляющие G₁ и G₂, параллельную и перпендикулярную наклонной плоскости. Модули этих составляющих определим по сле­дующим формулам:

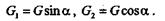
Составляющая G₂ уравновеши­вается реакцией N наклонной плос­кости. Таким образом,

 

Составляющая G₁ стремится сдвинуть тело вдоль наклонной плоско­сти. Полностью или частично эта составляющая уравновешивается силой трения; согласно второму закону трения скольжения, ее максимальное значение равно

где f — коэффициент трения скольжения тела по наклонной плоскости.

Для того чтобы тело, лежащее на наклонной плоскости, находилось в равновесии, движущая сила G₁ должна быть по модулю равна силе тре­ния F_тр, т. е.

откуда .

Если угол, который наклонная плоскость составляет с горизонтом, равен углу трения, то тело, лежащее на наклонной плоскости, будет под действием собственной силы тяжести либо равномерно скользить вниз, либо находиться в покое.

Для того чтобы тело, лежащее на наклонной плоскости, заведомо не скользило вниз под действием собственной силы тяжести, должно быть соблюдено условие .

Наклонной плоскостью с переменным углом наклона к горизонту пользуются для экспериментального определения угла трения  и коэф­фициента трения f (рис. 6.6).

Определим модуль силы Р, параллельной наклонной плоскости, в случае равномерного перемещения тела вверх по шероховатой наклонной плоскости (рис. 6.7).

51

 

Спроецируем силы, действующие на тело, на ось х.Составим урав­нение равновесия:

Так как

то

Определим модуль горизонтальной силы Р, которую надо прило­жить к телу для равномерного перемещения его вверх по шероховатой

наклонной плоскости (рис. 6.8).

Из треугольника аbс имеем

Применим геометрическое условие равновесия плоской системы сходящихся сил (размерами тела пренебрегаем) и по­строим замкнутый силовой многоугольник, соответствующий уравнению равновесия

Этот случай движения имеет место при взаимном перемещении винта и гайки с прямоугольной резьбой, так как резьбу винта можно рассматривать как наклонную плоскость, угол наклона которой равен углу подъема винтовой линии.

Трение в резьбе, имеющей треуголь­ный или трапецеидальный профиль, по­добно трению в клинчатом ползуне. По­этому рассмотрим клинчатый ползун с уг-

52

лом заострения 2 , нагруженный вертикальной силой Q (рис. 6.9). Опре­делим силу Р, необходимую для равномерного перемещения ползуна вдоль горизонтальных направляющих, если коэффициент трения сколь­жения равен f.

Составим два уравнения равновесия ползуна:

где F_тр — сила трения на каждой грани ползуна; N— нормальная реак­ция направляющей.

Решая эту систему уравнений и учитывая, что F_тр = fN,получим

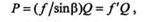
где f ' = f /sin   —приведенный коэффициент трения.

Соответствующий этому приведенному коэффициенту угол трения обозначим ф' и назовем приведенным углом трения, тогда

Очевидно, что f ' > f,следовательно, при прочих равных условиях трение в клинчатом ползуне больше трения на плоскости.

Понятие приведенного коэффициента трения условно, так как он из­меняется в зависимости от угла заострения клинчатого ползуна.

По аналогии с движением тела вверх по наклонной плоскости под действием горизонтальной силы для равномерного перемещения клинча­того ползуна по направляющим, наклоненным к горизонту под углом а, нужно приложить горизонтальную силу, равную

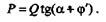
Трение в крепежной метрической резьбе подобно трению клинчатого ползуна с углом заострения 2  = 120°, для трапецеидальной резьбы угол

2 =150°.

53

Расчеты с учетом трения в резьбе рассматриваются при изучении предмета «Детали машин».

Наибольший угол, который составляет с горизонтом наклонная плоскость, образованная сыпучим телом, называется углом естест­венного откоса. Угол естественного откоса сыпучего тела равен углу трения между его частицами. Этот угол приходится принимать во внимание, например, при различных земляных работах.

Трение качения

Трением качения называется трение движения, при котором скоро­сти соприкасающихся тел в точках касания одинаковы по значению и направлению.

Если движение двух соприкасающихся тел происходит при одновре­менном качении и скольжении, то в этом случае возникает трение качения с проскальзыванием.

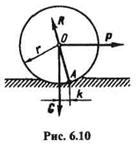
Рассмотрим качение без скольжения цилиндра весом G и радиусом r по горизонтальной опорной плоскости (рис. 6.10). Под давлением силы G произойдет деформация цилиндра и опорной плоскости в месте их сопри­косновения. Если сила Р не действует, то сила G будет уравновешиваться реакцией R опорной плоскости и цилиндр будет находиться в покое (ре­акция R будет вертикальна).

Если к цилиндру приложить небольшую силу Р, то он по-прежнему будет находиться в покое. При этом произойдет перераспределение дав­лений на опорную поверхность и полная реакция R пройдет через какую-то точку А и через точку О (согласно теореме о равновесии трех непарал­лельных сил).

При каком-то критическом значении силы Р цилиндр придет в дви­жение и будет равномерно перекатываться по опорной плоскости, а точка А займет крайнее правое положение. Отсюда видно, что трение качения в состоянии покоя может изменяться от нуля до какого-то максимального значения, причем максимальным оно будет в момент начала движения.

Обозначим k максимальное значение пле­ча силы G относительно точки А.Тогда в слу­чае равномерного перекатывания цилиндра (т. е. равновесия)

 

или

 

 

причем плечо силы Р вследствие незначитель­ности деформаций тел считаем равным радиу-

 

су r цилиндра (сила Р — горизонтальная). Из последнего равенства опре­делим силу, необходимую для равномерного качения цилиндра:

 

Максимальное значение плеча k называется коэффициентом трения качения;он имеет размерность длины и выражается в сантиметрах или миллиметрах.

Из полученной формулы видно, что усилие, необходимое для пере­катывания катка, прямо пропорционально его весу и обратно пропорцио­нально радиусу катка.

Коэффициент трения качения определяется опытным путем, его зна­чения для различных условий приводятся в справочниках.

Приведем ориентировочные значения коэффициентов k трения каче­ния для катка по плоскости (см):

Мягкая сталь по мягкой стали.................... 0,005

Закаленная сталь по закаленной стали .. 0,001

Чугун по чугуну.......................................... 0,005

Дерево по стали.......................................... 0,03...0,04

Дерево по дереву........................................ 0,05...0,08

Резиновая шина по шоссе........................... 0,24

Коэффициент трения качения практически не зависит от скорости движения тела.

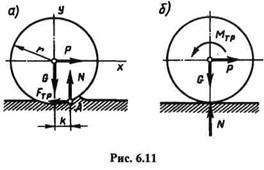
В ряде случаев при изучении трения качения активные и реактивные силы, действующие на каток, удобно представлять себе в ином виде (рис. 6.11, a, б).

Разложим полную реакцию R опорной поверхности на составляю­щие N и F_тр, тогда

 

где F_tp — сила трения качения, N — реакция, нормальная к недеформи-рованной опорной плоскости.

Составим три урав­нения равновесия катка:

Из этих уравнений имеем

                                  55

Введем обозначения Pr = M, Gk = M_три назовем М— момент каче­ния,

М_тр— момент трения.

Возможны следующие частные случаи движения катка:

а )М  М_тр, но P<F_тр— только качение;

б) М< М_тр, но P>F_тр— только скольжение;

в) М> М_тр, но P>F_тр— качение с проскальзыванием;

г) М< М_тр, но P<F_тр— состояние покоя.

Трение качения в большинстве случаев меньше трения скольжения, поэтому вместо подшипников скольжения широко применяют шариковые и роликовые подшипники качения.

На практике нередки случаи сочетания трения скольжения с трением качения, например в зубчатых зацеплениях или игольчатых подшипниках.

---

Дата добавления: 2018-04-15; просмотров: 1542; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!