Аналитические условия равновесия
Пространственной системы сходящихся сил
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система находится в равновесии, т. е. эквивалентна нулю, то равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей равны нулю, причем эти проекции равны сумме проекций составляющих.
|
|
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
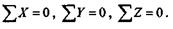
Эти условия формулируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточн 
о, чтобы алгебраическая сумма проекций всех сил на каждую из трех координатных осей равнялась нулю.
Пример 7.1. Груз G = 200 Н удерживается в равновесии горизонтальной веревкой АО и двумя веревками ВО и СО,плоскость которых наклонена к горизонтальной плоскости под углом 
=45° и образует с вертикальной плоскостью, проходящей через АО, прямой угол (рис. 7.3, а).Веревки ВО и СО образуют с этой вертикальной плоскостью углы 
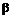= 30°. Определить натяжение веревок.
Решение. Рассмотрим равновесие узла О,к которому приложены четыре силы: G, RA, RB, RC. К пространствен-
60
ной системе четырех сходящихся сил применим аналитические условия равновесия и составим три уравнения равновесия:
Так как углы между реакциями RB, RC и осями координат х и z неизвестны, то для удобства проецирования каждую из этих сил разложим на две составляющие, как показано на рис. 7.3, б.Тогда
|
|
|
Проекции составляющей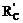 
на оси х и z равны нулю, так как эта составляющая перпендикулярна указанным осям;
Учитывая, что RВ=RC,получаем
откуда
|
|
Момент силы относительно оси
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (рис. 7.4). Червяк передает червячному колесу силу F, не лежащую в плоскости, перпендикулярной оси.
|
|
Разложим силу F на три взаимно перпендикулярные составляющие F1, F2 и F3. Составляющую F1 назовем окружной силой, составляющую F2 — осевой силой, а составляющую F3 — радиальной силой.
Составляющая F1 вызывает вращательное действие, которое измеряется произведением F1r; составляющая F2 стремится сдвинуть колесо вдоль оси, составляющая F3 стремится изогнуть ось колеса, а вращательное действие этих сил относительно оси равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следу-
661
|
|
ет принимать в расчет только составляющую F1, лежащую в плоскости, перпендикулярной оси, и не пересекающую ось.
Ранее было установлено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением. Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
|
|
|
Это определение поясняет рис. 7.5. Момент силы относительно оси условимся записывать следующим образом:
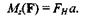
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, момент силы считаем отрицательным, если она стремится вызвать вращение по часовой стрелке.
Момент силы относительно оси не меняется при перемещении силы вдоль линии ее действия.
Момент силы относительно оса. равен нулю в двух случаях (не считая случаев, когда сила равна нулю или действует вдоль оси):
1) если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рис. 7.5, сила Fz);
2) если линия действия силы пересекает ось, так как при этом плечо равно нулю (см. рис 7.4, сила F3).
|
|
|
Дата добавления: 2018-04-15; просмотров: 464; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!