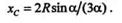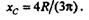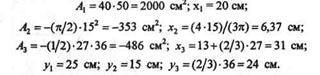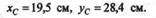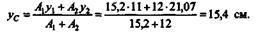Положение центра тяжести некоторых фигур
Прямоугольник.Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
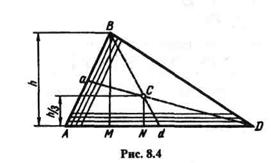
Треугольник.Пусть дан треугольник ABD (рис. 8.4). Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD.Центр тяжести каждой полоски будет лежать на медиане Вd,следователь-
71
|
|
|
|
но, на этой медиане будет лежать центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне АВ, увидим, что искомый центр тяжести лежит и на медиане aD, следовательно, центр тяжести площади треугольника лежит в точке пересечения его медиан. Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в отношении 1:2 от основания. Из подобия треугольников CNd и BMd получим
|
|
Следовательно, центр тяжести площади треугольника лежит на расстоянии одной трети высоты от каждого основания.
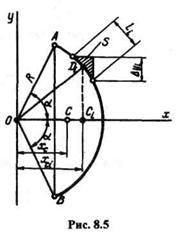
Дуга окружности. Возьмем дугу АВ окружности радиусом R с центральным углом 2  (рис. 8.5). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось х делила дугу пополам, тогда уC = 0 вследствие симметрии дуги относительно оси х. Определим xC.
(рис. 8.5). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось х делила дугу пополам, тогда уC = 0 вследствие симметрии дуги относительно оси х. Определим xC.
Разобьем дугу АВ на элементарные части li, одна из которых изображена на чертеже. Тогда, согласно § 8.2,
|
|
Дугу li, вследствие малости примем за отрезок прямой. Из подобия  ODiCi и элементарного
ODiCi и элементарного  S (на чертеже заштрихован) получим
S (на чертеже заштрихован) получим
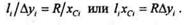
Тогда
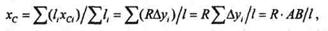
72
|
|
|
|
так как 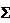
 yi =АВ, а
yi =АВ, а 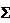 li =l — длина дуги АВ.Но АВ = 2Rsin
li =l — длина дуги АВ.Но АВ = 2Rsin  , а l = 2R
, а l = 2R  , следовательно,
, следовательно,
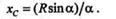
|
|
| При |
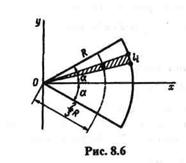
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2  (рис. 8.6). Проведем оси координат, как показано на чертеже, тогда уC = 0. Определим хС, для чего разобьем сектор на ряд элементарных секторов, каждый из которых вследствие малости дуги li примем за равнобедренный треугольник с высотой R.Тогда центр тяжести каждого элементарного сектора будет лежать на дуге радиуса 2R/3и задача определения центра тяжести сектора сведется к определению центра тяжести дуги окружности радиуса 2R/3, следовательно,
(рис. 8.6). Проведем оси координат, как показано на чертеже, тогда уC = 0. Определим хС, для чего разобьем сектор на ряд элементарных секторов, каждый из которых вследствие малости дуги li примем за равнобедренный треугольник с высотой R.Тогда центр тяжести каждого элементарного сектора будет лежать на дуге радиуса 2R/3и задача определения центра тяжести сектора сведется к определению центра тяжести дуги окружности радиуса 2R/3, следовательно,
|
|
| При |
|
|
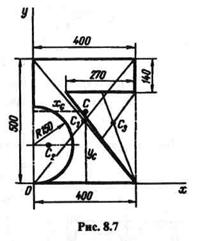
Пример 8.1. Определить положение центра тяжести тонкой однородной пластинки, форма которой и размеры в миллиметрах показаны на рис. 8.7.
Решение. Выберем оси координат, как показано на рис. 8.7. Представим себе заданную фигуру состоящей из трех частей: прямоугольника 400 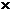 500, полукруга и треугольника, причем площади двух последних частей будем считать отрицательными. Тогда
500, полукруга и треугольника, причем площади двух последних частей будем считать отрицательными. Тогда
73
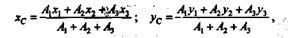
где
|
|
Подставив значения и произведя вычисления, получим
|
|
|
|
Пример 8.2. Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рис. 8.8.
Решение. Из курса черчения известно, что номер профиля проката соответствует наибольшему габаритному размеру его сечения, выраженному в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси у, то центр тяжести такого сечения лежит на этой оси, т. е. хC = 0. По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения
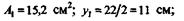
для швеллерного сечения
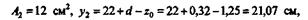
где d — толщина стенки швеллера; z0 — размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения ординаты центра тяжести всего сечения
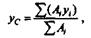
тогда
|
|
Раздел второй
КИНЕМАТИКА
Глава 9
КИНЕМАТИКА ТОЧКИ
Дата добавления: 2018-04-15; просмотров: 998; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

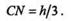
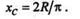
 /2 рад (полуокружность)
/2 рад (полуокружность)