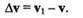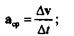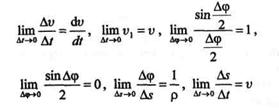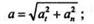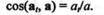Понятие о кривизне кривых линий
Как увидим в следующем параграфе, ускорение точки в криволинейном движении зависит от степени изогнутости ее траектории, т. е. от кривизны траектории.
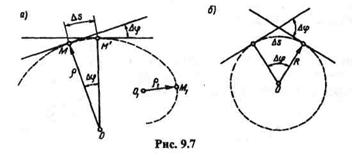
Рассмотрим криволинейную траекторию точки М (рис. 9.7, а).Угол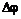 
между касательными к кривой в двух соседних точках называется углом смежности.
Кривизной кривой в данной точке называется предел отно-
85
|
|
шения угла смежности к соответствующей длине 
s дуги, когда последняя стремится к нулю. Обозначим кривизну k,тогда
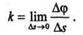
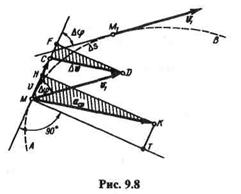
Рассмотрим окружность радиуса R (рис. 9.7, б). Так как
то
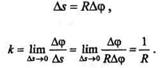
Следовательно, кривизна окружности во всех точках одинакова и равна
Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус 
такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности называется центром кривизны.
Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в этой же точке:
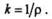
Очевидно, что кривизна прямой линии равна нулю, а радиус кривизны равен бесконечности:
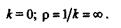
Теорема о проекции ускорения
На касательную и нормаль
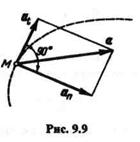
Проекция полного ускорения на нормаль к траектории называется нормальным ускорением; проекция полного ускорения на касательную к траектории называется касательным ускорением. Касательное ускорение иногда называют тангенциальным.
86
|
|
Теорема.Нормальное ускорение равно квадрату скорости, деленному на радиус кривизны траектории в данной точке, касательное ускорение — первой производной скорости по времени.
Пусть задано плоское движение точки М по траектории АВ (рис. 9.8). За время t точка перешла из положения М в положение М1,пройдя при этом путь s = OMM1.
Вектор приращения скорости за время 
t равен
|
|
Определим вектор среднего ускорения:
|
|
отложим этот вектор из точки М параллельно вектору v.
Спроецируем вектор аср на касательную и нормаль, точку D также спроецируем на касательную.
Рассмотрим подобные треугольники CDF и МКН.Из подобия этих треугольников имеем
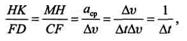
откуда
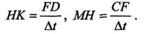
Перейдем к пределу при t,стремящемся к нулю (при этом 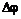и s также стремятся к нулю):
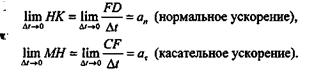
Вычислим первый предел при t,стремящемся к нулю:
87
так как
Вычислим второй предел при t, стремящемся к нулю:
так как
|
|
(предел второго слагаемого равен нулю, так как он представляет собой произведение конечных величин, умноженных на нуль).
Итак,
и теорема доказана.
Анализируя формулы касательного и нормального ускорений, можно видеть, что если нет изменения скорости по модулю, то 
; если нет изменения скорости по направлению (прямолинейное движение), то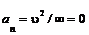 
. Отсюда следует, что касательное ускорение характеризует изменение скорости только по модулю, а нормальное — только по направлению.
|
|
|
Зная касательное и нормальное ускорения, можно вычислить модуль и направление полного ускорения по формулам:
88
|
|
|
|
|
|
| модуль ускорения |
| направление ускорения |
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. Из § 2.3 нам известно, что если оси взаимно перпендикулярны, то проекции вектора на эти оси и его составляющие, направленные по этим осям, равны по модулю.
Касательное, нормальное и полное ускорения изображены на рис. 9.9.
Если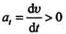 
то векторы касательного ускорения и скорости направлены в одну сторону и движение будет ускоренным. Если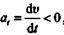 
вектор касательного ускорения направлен в сторону, противоположную вектору скорости, и движение будет замедленным.
Вектор нормального ускорения всегда направлен к центру кривизны, поэтому это ускорение иначе называют центростремительным.
Пример 9.5. Точка обода маховика в период разгона движется согласно уравнению s = 0,1t3 (t— в секундах, s — в метрах). Радиус маховика равен 2 м. Определить нормальное и касательное ускорения точки в момент, когда ее скорость 
=30 м/с.
|
|
|
Решение. Для определения скорости вычислим производную пути по времени:
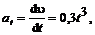
откуда
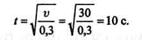
Для этого момента следует определить нормальное и касательное ускорения точки. Находим касательное ускорение как производную скорости по времени:
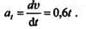
Подставляем в выражение для касательного ускорения значение t = 10 с:
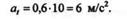
Нормальное ускорение точки определяем по формуле
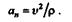
Для момента времени t =10 с находим
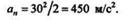
89
Дата добавления: 2018-04-15; просмотров: 686; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!