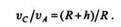Вращение вокруг неподвижной оси

Движение, при котором по крайней мере две точки твердого тела или неизменяемой системы остаются неподвижными, называется враща­тельным; прямая линия, соединяющая эти две точки, называется осью вращения. В определении вращательного движения говорится о неизменяемой системе, потому что ось вращения может лежать и вне тела.

Вращательное движение в технике встречается весьма часто. В по­давляющем большинстве механизмов и машин имеются звенья, которые совершают вращательное движение, например валы, зубчатые колеса, кривошипы и т. д. Заметим, что понятие вращательного движения может относиться только к телу, но не к точке; так, например, движение точки по окружности есть не вращательное движение, а криволинейное.

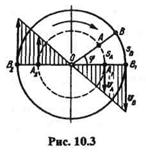
Рассмотрим диск, вращающийся вокруг оси, перпендикулярной плоскости чертежа (рис. 10.3). Точка О — след этой оси. Очевидно, что траектории точек вращающегося тела есть окружности различных радиу­сов, расположенные в плоскостях, перпендикулярных оси вращения, с центрами, лежащими на этой оси.

Пусть за время t диск повернулся на угол 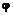. При этом точка А про­шла путь s_A, а точка В — путь s_B. Так как точки, находящиеся на различ­ном расстоянии от оси вращения, за один и тот же промежуток времени проходят разные пути, то, следовательно, они имеют разные скорости и ускорения.

Итак, при вращательном движении тела точки его, находящиеся на различном расстоянии от оси вращения, имеют неодинаковые траекто­рии, скорости и ускорения.

Отсюда следует, что линейное перемещение (путь), линейные ско­рость и ускорение точек не могут характеризовать вращательное движе­ние тела в целом. Вращательное движение тела можно характеризовать углом ф, на который повернулось тело за данный промежуток времени. Этот угол называется угловым перемещением тела. Угловое перемещение выражается в радианах (рад) или оборотах (об); в последнем случае угловое перемещение обозначают N.Для установления зависимости между 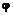 и N составим пропорцию:

1 об — 2 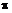 рад,

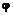N o6 — рад,

откуда

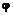 = 2 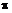N рад,

где N— число оборотов тела.

1101

Угловое перемещение тела есть функция времени, следовательно, закон вращательного движения в самом общем виде запи­шется так:

Из рис. 10.3 видно, что путь любой точки вращающегося тела

где r— расстояние точки от оси вращения.

Скорость любой точки тела определяется так:

(r вынесли за знак производной, так как для данной точки твердого тела эта величина постоянна).

Выражение 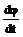— обозначим ю и назовем угловой скоростью.

Угловая скорость есть кинематическая мера движения вращающегося тела, характеризующая быстроту его углового перемещения:

Угловая скорость равна первой производной углового перемещения по времени.

Единица угловой скорости

Скорость точки в каждый момент времени прямо пропорциональна ее расстоянию от оси вращения, следовательно, график скоростей точек, например диаметра В₁В₂,будет представлять собой два треугольника (рис 10.3). Очевидно, что вектор скорости точки вращающегося тела направлен перпендикулярно радиусу, соединяющему эту точку с осью вращения. Если точка лежит на поверхности вращающегося тела, то ее скорость называют окружной.

В технике часто скорость вращения выражают в оборотах в минуту, обозначают буквой п и называют частотой вращения. Установим зависимость между угловой скоростью и частотой вращения, выраженными соответственно в рад/с и мин ^-1. Запишем пропорцию:

102

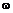рад — 1 с,

 2 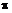п рад — 60 с.

Из пропорции найдем

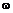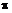 = п /30 рад/с,

где п — частота вращения тела, об/мин или мин ^-1.

Пример 10.2. Сколько времени (мин) продлится обточка вала диаметром d = 180 мм и длиной l = 1000 мм, если обточка ведется за один проход резца, подача резца за один оборот изделия s_об= 0,5 мм/об, а скорость резания = 135 м/мин.

Решение. Прежде всего определим угловую скорость со и частоту вращения п вала

Далее определим подачу резца в минуту:

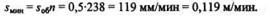
Разделив длину обрабатываемой поверхности на минутную подачу резца, определим машинное время, необходимое для обточки вала:

Пример 10.3. Проект создания мировой ретрансляционной системы телеви­дения заключается в запуске трех искусственных спутников Земли таким образом, чтобы они образовали равносторонний треугольник неподвижный по отношению к Земле. С какой скоростью должны двигаться спутники по круговой орбите, расположенной в плоскости экватора, если известно, что они будут летать на вы­соте h = 35 800 км? Радиус Земли на экваторе R = 6370 км (рис 10.4). Определить также окружную скорость точки на экваторе.

Решение. Если спутники будут неподвижны по отношению к Земле, то мож­но считать, что вместе с Землей они составляют неизменяемую систему. Опреде­лим окружную скорость _A  точки А, находящейся на экваторе Земли по формуле

Угловая скорость вращения Земли вокруг своей оси равна

Тогда скорость точки А будет равна

Так как спутники составляют вместе с Зем­лей неизменяемую систему, вращающуюся вокруг земной оси, то скорости точек этой системы пря­мо пропорциональны их расстояниям от оси вра­щения:

103

Отсюда определим искомую скорость спутников: Дата добавления: 2018-04-15; просмотров: 676; Мы поможем в написании вашей работы! Поделиться с друзьями: ⇐ Предыдущая19202122232425262728Следующая ⇒ Мы поможем в написании ваших работ! . . © 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.024)