Понятие о плоскопараллельном движении

Плоскопараллельным движением твердого тела называ­ется такое движение, при котором все точки тела перемещаются в плоско­стях, параллельных какой-то одной плоскости, называемой основной.

Примерами плоскопараллельного движения могут служить движение колеса на прямолинейном участке пути, движение шатуна кривошипно-ползунного механизма.

Из определения плоскопараллельного движения следует, что любая прямая АВ,проведенная в теле перпендикулярно основной плоскости, движется поступательно (рис. 12.1). Для определения движения тела на каждой прямой, перпендикулярной основной плоскости, надо знать дви­жение только одной точки. Взяв эти точки в одной плоскости Q,парал­лельной основной, получим сечение S,движение которого определяет движение тела. Но плоское движение сечения S вполне определяется движением двух любых его точек С и D или отрезка CD.Таким образом, вопрос о плоскопараллельном движении тел сводится к вопросу о дви­жении отрезка прямой в плоскости, параллельной основной.

Плоскопараллельное движение изучается двумя методами: 1) методом мгно­венных центров скоростей и 2) методом разложения шюскопараллелъного дви­жения на поступательное и вращательное.

11115

Метод мгновенных центров скоростей

В основе этого метода лежит следующая теорема: всякое плоскопа­раллельное перемещение твердого тела может быть получено одним вращением около оси, перпендикулярной основной плоскости.

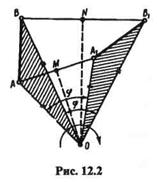
Пусть отрезок, определяющий плоскопараллельное движение тела, за конечный промежуток времени переместился из положения АВ в положе­ние A₁B₁(рис. 12.2).

Соединим точки А и А₁, В и В₁прямыми линиями и из середин полу­ченных отрезков (точек M и N)восставим перпендикуляры до их взаим­ного пересечения в точке О.Эту точку соединим прямыми линиями с концами отрезков АВ и А₁В₁и получим два конгруэнтных (равных) тре­угольника, имеющих общую вершину О:

Треугольник АОВ совмещается с треугольником А₁ОВ₁ путем пово­рота на угол 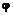 вокруг точки О,называемой центром конечного поворота. Точка О есть след оси конечного поворота, перпендикуляр­ной основной плоскости. Таким образом, отрезок АВ,определяющий плоскопараллельное движение тела, перемещается в любое новое поло­жение путем одного вращения вокруг оси конечного поворота. Теорема доказана.

Приведенное доказательство будет справедливо и в том случае, если перемещение тела произойдет за бесконечно малый промежуток времени t.В пределе при t,стремящемся к нулю, вращение будет происходить вокруг мгновенной оси. След мгновенной оси вращения на плоско­сти фигуры называют м г н о в е и н ы м центром скоростей. Оче­видно, что скорость точки, являющейся в данный момент мгновенным центром скоростей, равна нулю. Угловая скорость 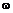, с которой происхо­дит мгновенное вращение, называется мгновенной угловой скоростью.

Точка неподвижной плоскости, совпа­дающая в данный момент времени с мгно­венным центром скоростей плоской фигуры, называется мгновенным центром вращения.

Если прямая АВ движется параллельно самой себе, то можно полагать, что тело вращается вокруг оси, удаленной в беско­нечность, иначе говоря, поступательное движение можно рассматривать как враща­тельное по кругу бесконечно большого ра­диуса.

116

Таким образом, плоскопараллельное движение тела может осуще­ствляться путем последовательных мгновенных непрерывных поворотов вокруг мгновенных осей вращения.

Заметим, что методом мгновенных центров скоростей можно поль­зоваться только при определении скоростей точек плоской фигуры, но не при определении траекторий и ускорений этих точек.

---

Дата добавления: 2018-04-15; просмотров: 593; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!