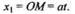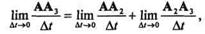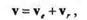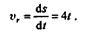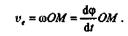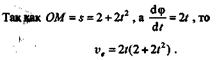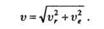Понятие о сложном движении точки

⇐ ПредыдущаяСтр 27 из 72Следующая ⇒

До сих пор рассматривалось движение точки по отношению к одной системе координат, которую полагали неподвижной. В мире все находится в непрерывном движении, и неподвижная система координат в действительности не существует. Поэтому нередко возникает необходимость рассматривать движение точек одновременно по отношению к двум системам отсчета, одна из которых условно считается неподвижной, а вторая определенным образом движется по отношению к первой. Движение точки в этом случае называется сложным.

Движение точки по отношению к неподвижной системе координат называется абсолютным. Движение точки по отношению к подвижной системе координат называется относительным. Движение подвижной системы координат по отношению к неподвижной называется переносным.

Абсолютное движение точки является сложным и состоит из относительного и переносного движений.

111

Поясним изложенное с помощью рис. 11.1.

Пусть хОу — подвижная система координат, перемещающаяся в плоскости чертежа равномерно поступательно вдоль оси х;точка А равномерно перемещается вверх по оси у.Если будет совершаться только относительное движение, то точка перейдет из положения А в положение А₁.Если будет совершаться только переносное движение, то точка из положения А попадет в положение А₂.Если же одновременно совершаются и относительное и переносное движения, то точка за этот же промежуток времени перейдет из положения А в положение А₃.

Пользуясь определением переносного и относительного движений, а также рассмотренным выше примером, можно указать на следующий метод изучения этих движений. Если необходимо изучить относительное движение точки, то следует мысленно остановить переносное движение, если необходимо изучить переносное движение точки, то следует мысленно остановить относительное движение.

Пример 11.1.Стержень ОА вращается вокруг оси О в плоскости рисунка по закону ;по стержню движется точка М по закону ОМ = at.Найти траекторию абсолютного движения точки М (рис. 11.2).

Решение. Выберем неподвижную систему координат хОу и подвижную систему х₁Оу₁, неизменно связанную со стержнем ОА. В таком случае переносным движением будет вращение подвижных осей вместе с мысленно закрепленной на них в каждый момент точкой М вокруг точки О,а относительным — движение точки М вдоль стержня.

Уравнение относительного движения будет иметь вид

Уравнение переносного вращательного движения запишется так:

Определим уравнение абсолютного движения точки в координатной форме, для чего координаты х и у в неподвижной системе отсчета хОу выразим как функции времени t.

Из рис. 11.2 имеем:

112

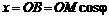
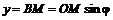
или, подставляя значения 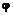и ОМ, получим:

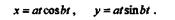
Чтобы определить уравнение траектории абсолютного движения точки, исключим из уравнений движения время t, для чего разделим второе уравнение на первое:

откуда

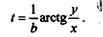
Кроме того, возведя уравнения движения в квадрат и сложив их, получим

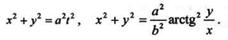
Таково уравнение траектории абсолютного движения точки М. Эта траектория есть архимедова спираль.

Теорема о сложении скоростей

Скорость точки в абсолютном движении называется абсолютной. Скорость точки в относительном движении называется относительной. Скорость рассматриваемой точки, мысленно закрепленной в данный момент на подвижной системе координат, называется переносной. Связь между этими скоростями устанавливает теорема о сложении скоростей.

Теорема.Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей.

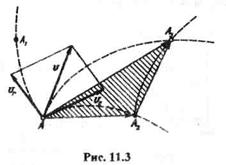
Пусть за время t точка перешла из положения А в положение А₃, двигаясь по траектории абсолютного движения, т. е. по дуге АА₃(рис. 11.3). Если бы имело место только относительное движение, то точка перешла бы в положение А_1;если бы только переносное, то точка перешла бы в положение А₂. Можно представить, что точка А перешла в положение А₃двигаясь сначала только по траектории переносного движения (дуга АА₂),а затем только по траектории относительного дви-

113

жения (дуга А₂А₃,равная дуге АА₁).

Соединив точки А, А₂и А₃хордами, получим следующую зависимость между векторами перемещений точки А:

Разделим все члены равенства на t и перейдем к пределу при t, стремящемся к нулю:

что дает

где v — вектор абсолютной скорости; v_е — вектор переносной скорости; v_r — вектор относительной скорости. Теорема доказана.

Пример 11.2.Стержень ОА (рис. 11.4) вращается в плоскости чертежа вокруг неподвижной точки О по закону 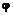= r².По стержню равноускоренно движется ползун М, удаляясь от точки О.Движение ползуна определяется уравнением

(s — в метрам, t—в секундах). Найти абсолютную скорость ползуна в момент t= 1 с.

Решение. Выберем неподвижную систему координат хОу;подвижной системой будем считать стержень. В таком случае относительным движением является движение ползуна М по стержню. Следовательно, относительная скорость направлена вдоль стержня и равна

В момент t = 1 с относительная скорость будет по модулю равна _r₁= 4 м/с.

Переносным движением является вращательное движение стержня ОА с мысленно закрепленным на нем в данный момент ползуном, поэтому переносная скорость _e ползуна направлена перпендикулярно стержню, причем ее значение определяется по формуле

Полагая t= 1с, получим ₁_e - 8 м/с.

Так как относительная и переносная скорости взаимно перпендикулярны, а на основании теоремы о сложении скоростей v= v_r + v_е, то

114

Подставляя значения скоростей при t= 1 с, получим

Глава 12

ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ

ТВЕРДОГО ТЕЛА

Дата добавления: 2018-04-15; просмотров: 539; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 22 23 24 25 262728 29 30 31 Следующая ⇒

Мы поможем в написании ваших работ!