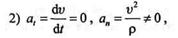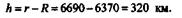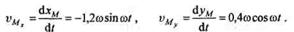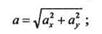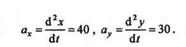Виды движения точки в зависимости от ускорений

Анализируя выведенные формулы касательного и нормального уско­рений, можно установить следующие виды движения точки:

в этом случае движение неравномерное ( const) криволи­нейное ( );

 

в этом случае движение равномерное ( =const) криволиней­ное ( );

в этом случае движение неравномерное( const) прямоли­нейное ( );

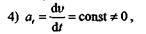
в этом случае движение равнопеременное (криволинейное, если а_п , прямолинейное, если а_п = 0);

 

в этом случае движение равномерное прямолинейное, кото­рое является единственным видом движения без ускорения.

Формулы и графики равномерного

Движения точки

      

   Как было установлено ранее, при равномерном движении касатель­ное ускорение а_t . Следовательно, модуль скорости точки при равномерном движении есть величина постоянная:

Отсюда

90

 

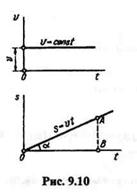
Интегрируя это выражение, получаем

где s₀— начальное расстояние.

Итак, формулы равномерного движения точки имеют следующий вид:

Графики скорости и пути равномерного движения показаны на рис. 9.10, причем предполагается, что s₀= 0.

Нетрудно показать, что скорость точки при равномерном движении пропорциональна тангенсу угла  между прямолинейным графиком этого движения и положительным направлением оси времени:

где _s— масштаб пути, выражаемый в м/мм; _t — масштаб времени, вы­ражаемый в с/мм.

Пример 9.6.Первый искусственный спутник, запущенный 4 октября 1957 г. в нашей стране, имел скорость v,равную 7,78 км/с, и период обращения, равный 1 ч 30 мин, или 5400 с. Определить высоту полета спутника над поверхностью Земли, полагая его орбиту круговой, а движение равномерным. Радиус Земли принять равным R = 6370 км.

Решение. Обозначим r — радиус орбиты спутника, проведенный из центра Земли; h— искомую высоту спутника над поверхностью Земли (рис. 9.11).

Путь s,проходимый спутником за один период обращения, равен произве­дению времени Т,затраченного на один оборот, на скорость движения спутни­ка. С другой стороны, этот же путь равен длине окружности радиуса r.

Таким образом,

91

откуда

Далее находим искомую высоту полета:

 

Формулы и графики равнопеременного

Движения точки

Как было установлено ранее, при равнопеременном движении каса­тельное ускорение есть величина постоянная:

Отсюда

Интегрируя это выражение, получаем

где ₀— начальная скорость.

Формула скорости в окончательном виде

Так как

то, интегрируя это выражение, получаем формулу перемещений (расстоя­ний от начального положения)

где s₀ — начальное расстояние.

Полагая s₀= 0, запишем формулы равнопеременного движения точки:

 

Если точка совершает криволинейное движение, то она имеет нор­мальное ускорение

а модуль ее полного ускорения определится по формуле

92

Если точка движется прямолинейно, то а_n=0, а полное ускорение равно касательному: а = а_t.

В равноускоренном дви­жении направление вектора ускорения совпадает с на­правлением вектора скоро­сти; в равнозамедленном движении вектор ускорения направлен в сторону, об­ратную вектору скорости.

Формулу перемещений (расстояний от начала от­счета) преобразуем, исклю­чив из нее время t. Из фор­мулы скорости имеем

тогда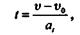

После преобразований получим

В некоторых случаях при решении задач удобно пользоваться фор­мулой перемещений равнопеременного движения в ином виде. Так как

Графики ускорения, скорости и перемещения точки при прямоли­нейном равнопеременном движении представлены на рис. 9.12.

Кривая перемещений (расстояний) при равнопеременном движении представляет собой параболу.

Из высшей математики известно, что если построить график какой-то функции у =f(x),то в любой точке этого графика

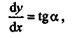
93

где — угол, который составляет в этой точке касательная к кривой с положительным направлением оси абсцисс.

Применяя это положение к изображенным на рис. 9.12 графикам движения точки и учитывая масштабы пути и времени, получим

 

где ₁ — угол между касательной к графику перемещения и положитель­ным направлением оси времени; _s— масштаб пути, выражаемый в м/мм; _t — масштаб времени, выражаемый в с/мм.

Из изложенного следует, что если касательная к кривой перемеще­ний составляет острый угол с положительным направлением оси времени, то в этот момент скорость точки положительная; при тупом угле скорость точки в этот момент отрицательная. Если касательная в какой-то точке кривой перемещений параллельна оси времени, то скорость точки в этот момент равна нулю (рис. 9.12).

Аналогичная связь имеется между графиками скорости и ускорения прямолинейного движения точки, а именно

 

где  — угол между касательной к графику скорости и положительным направлением оси времени; ( 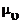— масштаб скорости, выражаемый в (м/с)/мм.

Нужно обратить внимание на то, что кривая перемещений при рав­ноускоренном движении имеет выпуклость, направленную вниз (вторая производная перемещения по времени положительна), а при равнозамед-ленном движении — выпуклость, направленную вверх (вторая производ­ная перемещения по времени отрицательна).

Пример 9.7. Вагон скатывается по наклонной плоскости с ускорением а = 0,2 м/с². Какую скорость разовьет вагон в конце наклонной горки, длина кото­рой 250 м? Начальная скорость вагона ₀= 1 м/с.

Решение. Для определения скорости движения вагона в конце наклонной горки применим формулу

Из этой формулы найдем

Подставляя значения величин и извлекая квадратный корень, получаем

94

Теорема о проекции скорости

На координатную ось

Если движение точки за­дано естественным способом, то скорость ее находят как первую производную переме­щения по времени; если дви­жение точки задано в коорди­натной форме, то с помощью теоремы о проекции скорости на координатную ось.

Теорема.Проекция ско­рости на координатную ось равна первой производной от соответствующей коорди­наты по времени.

Пусть плоское движение точки М задано координатным способом уравнениями движения

За время t точка перешла из положения М положение М₁ (рис. 9.13). Если бы точка двигалась по хорде равномерно, то ее условная скорость была бы равна

Спроецируем вектор v_n и точку М на ось х,тогда

Так как

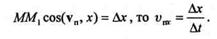
Перейдем к пределу при t, стремящемся к нулю:

Так как скорость v_n в пределе дает истинную скорость, то предел, стоящий в левой части равенства, дает проекцию истинной скорости на ось х,а правая часть есть первая производная от абсциссы х по времени, следовательно,

95

теорема доказана. Аналогично,

Зная две проекции скорости, можно найти ее модуль и направление по формулам:

модуль скорости

направление скорости

Пример 9.8.Найти модуль скорости середины М шатуна кривошипно-пол-зунного механизма и скорости ползуна В, если ОА=АВ = 0,8 м, а угол = 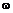t, где  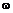— постоянная величина, a t выражается в секундах (см. рис. 9.3)

Решение. Для решения задачи воспользуемся уравнениями движения точки Ми ползуна В, полученными в примере 9.1:

Определим модуль скорости точки М:

Для определения скорости точки М применим теорему о проекции скорости на координатную ось, в результате чего получим

Так как ползун В движется прямолинейно, то для определения модуля ско­рости его движения продифференцируем уравнение движения по времени, в ре­зультате чего получим

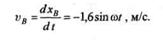
Теорема о проекции ускорения

На координатную ось

Если движение точки задано естественным способом, то ее ускоре­ние определяют с помощью теоремы о проекции ускорения на касатель-

96

ную и нормаль; если движение точки задано координатным способом — то с помощью теоремы о проекции ускорения на координатную ось.

Теорема.Проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени.

Из доказанной в предыдущем параграфе теоремы видно, что проек­ция скорости точки на координатную ось равна скорости проекции точки на ту же ось.

Аналогичное положение будет справедливо и для ускорения точки, т. е. проекция ускорения точки на координатную ось равна ускорению проекции точки на ту же ось. Так как проекции точек на оси движутся прямолинейно, то, согласно § 9.5,

 

Зная две проекции ускорения, можно найти модуль и направление полного ускорения по формулам: модуль ускорения

направление ускорения

 

Пример 9.9. Движение точки определяется уравнениями

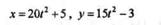
(t — в секундах, х и у — в метрах). Определить модуль и направление скорости и ускорения в момент времени t = 2 с.

Решение. Для определения модуля и направления скорости точки применим теорему о проекции скорости на координатную ось. Продифференцировав по времени уравнения движения точки, получим:

 

Модуль скорости точки определим по формуле

Подставив значение времени t = 2с, получим

Направляющий косинус определим по формуле

Для определения модуля и направления ускорения точки применим теорему о проекции ускорения на координатную ось. Второй раз продифференцировав по времени уравнения движения точки, получим:

97

 

Модуль ускорения точки определяем по формуле

 

Направляющий косинус определится по формуле

Угол между векторами v, а и осью х будет углом первой четверти, так как

есть величина положительная.

Так как направление вектора скорости в любой момент времени остается не­изменным, то движение точки является прямолинейным и полное ее ускорение можно определить по формуле

Глава 10

---

Дата добавления: 2018-04-15; просмотров: 863; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!