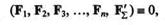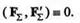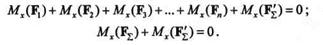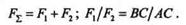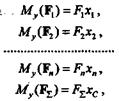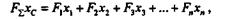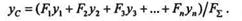Теорема о моменте равнодействующей

Относительно оси (теорема Вариньона)

Теорема. Момент равнодействующей относительно оси равен алгебраической сумме моментов составляющих сил относительно той оке оси.

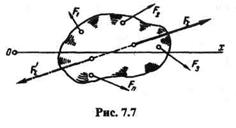
Пусть даны пространственная система п произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы F (рис. 7.7):

Приложим к телу другую систему сил, равнодействующая которой 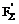по модулю равна силе 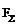и направлена по той же линии действия в противоположную сторону.

Сила 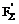для данной системы является уравновешивающей силой и вместе с данными силами образует уравновешенную систему

также

Так как обе записанные выше системы эквивалентны нулю, т. е. уравновешены, то можно применить к ним любое условие равновесия, например

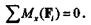
Запишем это условие для обеих систем:

Так как правые части этих равенств равны, то равны будут и левые:

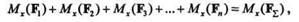
поскольку члены М_х( 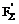)взаимно уничтожились.

Итак,

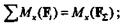
теорема доказана.

Глава 8

ЦЕНТР ТЯЖЕСТИ

Центр параллельных сил

Центром параллельных сил называется такая точка на линии действия равнодействующей системы параллельных сил, через которую

проходит равнодействующая и в том случае, если все силы системы повернуть вокруг их точек приложения на один и тот же угол, сохраняя параллельность сил.

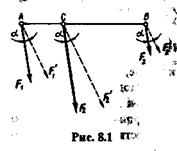
Покажем существование центра параллельных сил на системе двух сил F₁ и F₂ (рис. 8.1). На основании теоремы о сложении двух параллельных сил, направленных в одну сторону, определим равнодействующую этих сил и положение ее линии действия по формулам

Нетрудно видеть, что точка С, лежащая на линии АВ, соединяющей точки приложения данных сил, является центром двух параллельных сил F₁ и F₂, так как при повороте их на один и тот же угол а отношение плеч ВС и СА не изменится и равнодействующая также пройдет через точку С.

Если дана система п параллельных сил, то равнодействующую этой системы можно найти, последовательно попарно складывая все силы. На линии действия равнодействующей системы параллельных сил также будет существовать точка, обладающая свойством центра параллельных сил. Выведем формулы для определения координат центра системы п параллельных сил.

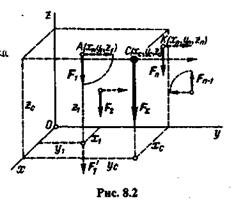
Пусть даны пространственная система п параллельных сил и равнодействующая этой системы. Выберем систему осей координат и обозначим координаты точек приложения сил данной системы и координаты точки приложения равнодействующей (рис. 8.2).

Запишем моменты сил данной системы относительно оси у.Для того чтобы легче представить, чему равен момент силы относительно оси, следует мысленно перенести силу вдоль линии действия до положения, когда точка приложения силы окажется в плоскости координатных осей (сила 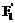на рис. 8.2):

Применим доказанную в предыдущем параграфе теорему о моменте равнодействующей относительно оси. Тогда

откуда

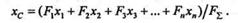
Записав моменты сил относительно оси х и вновь применив теорему о моменте равнодействующей, получим

Для определения координаты z_С повернем все силы системы вокруг их точек приложения в одну сторону, чтобы силы стали параллельны оси у.При этом точка С не изменит своего положения, так как она является центром параллельных сил данной системы.

Запишем моменты всех сил относительно оси х и применим теорему о моменте равнодействующей, в результате чего получим

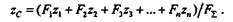
Равнодействующая системы параллельных сил равна их алгебраической сумме, т. е. F = F_i.Применив сокращенную форму записи, получим формулы для определения координат центра параллельных сил в следующем виде:

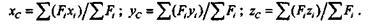
Заметим, что в выведенных формулах силы и моменты сил берут со знаком по ранее установленным правилам.

Дата добавления: 2018-04-15; просмотров: 1244; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒

Мы поможем в написании ваших работ!