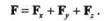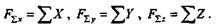Проекция силы на ось в пространстве
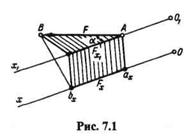
Определение проекции силы на ось остается прежним (см. § 2.3). Если сила и ось не лежат в одной плоскости, то проецирующие перпендикуляры также не лежат в одной плоскости (рис. 7.1).
Для того чтобы определить, чему равна проекция силы F на ось Ох,следует мысленно провести через начало или конец силы ось O1x1,параллельную данной оси Ох,тогда Fx = Fcos  , так как Fx = Fx1.
, так как Fx = Fx1.
Правило знаков для проекции остается прежним.
Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину.
Если вектор силы лежит в плоскости, перпендикулярной оси,то его проекция на эту ось равна нулю.
Разложение силы по трем осям координат
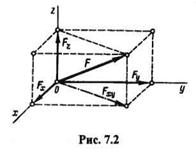
Пусть дана сила F(рис. 7.2). Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F. Из конца этого
|
|
|
|
58
|
|
| вектора опустим перпендикуляр на плоскость ху и разложим силу F на составляющие Fxy и Fz, а составляющую Fxy — на составляющие Fx и Fу.Тогда |
Достроим полученное изображение до параллелепипеда, у которого составляющие Fx, Fy, Fz являются ребрами, а сила F — диагональю.
Из изложенного можно сделать такой вывод: равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах.
Из рис. 7.2 видно, что в случаях разложения силы F по трем взаимно перпендикулярным направлениям х, у, z составляющие Fx, Fy, Fz равны по модулю проекциям силы F на эти оси. Эти проекции обозначим Fx, Fy, Fz.
Зная проекции силы на три взаимно перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы
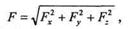
направляющие косинусы
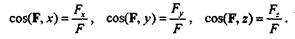
Аналитический способ определения
Равнодействующей пространственной системы
Сходящихся сил
Дана пространственная система п сходящихся сил. Поместим начало координат в точке пересечения линий их действия и разложим каждую силу данной системы на три взаимно перпендикулярные составляющие, направленные по осям координат, предварительно перенеся все силы вдоль линий их действия в одну точку.
Вместо данной системы п сходящихся сил мы получим эквивалентную ей систему 3п сил, из которых п сил действуют по оси х, п сил — по оси у и п сил — по оси z.
Равнодействующая сил, направленных по оси х,равна их алгебраической сумме; то же можно сказать о силах, направленных по осям у и z. Таким образом, систему 3п сил заменим эквивалентной ей системой трех сил.
Проекции силы на три взаимно перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны
59
|
|
Равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление вектора равнодействующей (см. § 7.3).
Дата добавления: 2018-04-15; просмотров: 1213; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!