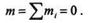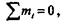Условие равновесия плоской системы пар
|
|
| Поэтому условие равновесия плоской системы пар в общем виде будет выглядеть так: |
|
|
Применяя доказанную в предыдущем параграфе теорему к плоской системе пар, находящейся в равновесии, запишем
а формулируется следующим образом: для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю.
34
Опоры и опорные реакции балок
Опоры балок по их устройству могут быть разделены на следующие три основных типа (рис. 4.8): 1) шарнирно-подвижная (опора А),2) шар-нирно-неподвижная (опора В); 3) жесткая заделка (опора С).
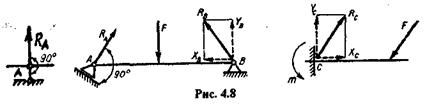
Применим правило для определения направления реакций связей (см. § 1.5).
Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю (одно неизвестное).
Шарнирно-неподвижная опора допускает только поворот вокруг оси шарнира и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и направление ее заранее не известны (два неизвестных). Обычно при решении задач такую реакцию раскладывают на две взаимно перпендикулярные составляющие, не известные по модулю, но известные по направлению.
Жесткая заделка (защемление) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой, не известной по модулю и направлению, и реактивным моментом (три неизвестных). Реактивную силу, не известную по направлению, раскладывают на две взаимно перпендикулярные составляющие.
|
|
|
Если при решении задачи реактивная сила или реактивный момент получатся отрицательными, то их действительное направление противоположно принятому.
Кроме перечисленных выше трех основных типов опор балок в конструкциях нередко балка свободно опирается на плоскость (поверхность) или на ребро призмы. В этих случаях направление реакций определяют по правилам, изложенным в § 1.5.
На рис. 4.8. (слева) показан другой способ условного изображения шарнирно-подвижной опоры.
35
|
|
|
|
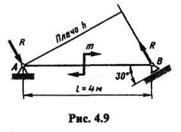
Пример 4.1.Горизонтальная балка длиной l = 4 м закреплена на опорах (рис. 4.9) и нагружена парой сил с моментом т = 420 Н 
м. Не учитывая силу тяжести балки, определить реакции опор А и В.
Решение. Отбросим опоры, заменив их реакциями, и рассмотрим равновесие балки. Так как пару сил можно уравновесить только парой, то реакцииR опор А и В должны образовывать пару сил, причем реакция шарнирно-подвижной опоры В перпендикулярна опорной плоскости.
|
|
|
Применим условие равновесия плоской системы пар и составим уравнение равновесия:
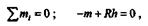
где h=lcos30о.
Отсюда R = m/h = m/(lcos30°) = 420/(4 0,866)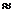 
120 Н.
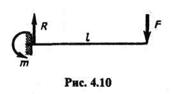
Пример 4.2.Консольная балка (рис. 4.10) длиной l = 2 м нагружена на конце силой F = 3000 Н. Не учитывая силу тяжести балки, определить реакции заделки.
Решение.Отбросим заделку, заменив ее реакциями, и рассмотрим равновесие балки. Реакции заделки представляют собой реактивную силу R и реактивный момент т. Так как реактивный момент т может быть уравновешен только парой сил, то нагрузка F и реакция R должны образовывать пару, следовательно,
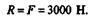
Далее применим условие равновесия плоской системы пар и составим уравнение равновесия:
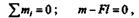
откуда m = Fl = 3000 
2 = 6000 Н м.
Глава 5
ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО
РАСПОЛОЖЕННЫХ СИЛ
Дата добавления: 2018-04-15; просмотров: 1369; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!