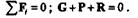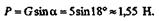Аналитические условия равновесия
Плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит, и проекции равнодействующей на оси координат равны нулю:
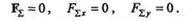
Учитывая, что
|
|
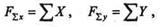
| получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил: |
Формулируются эти условия следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например, модуль и направление одной силы или модули двух сил, направления которых известны, и т. п.
Выведенные условия равновесия справедливы для любых осей координат, но для упрощения решения задач рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум взаимно перпендикулярным составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получится отрицательной, то это значит, что действительное ее направление противоположно направлению, принятому на рисунке.
|
|
|
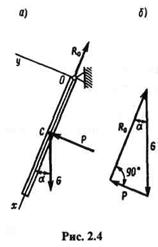
Пример 2.2. Однородная прямоугольная пластинка силой тяжести G = 5 Н подвешена так, что может свободно вращаться вокруг горизонтальной оси, проходящей вдоль одной из ее сторон. Равномерно дующий ветер удерживает ее в наклонном положении под углом 
=18° к вертикальной плоскости. Определить равнодействующую Рдавлений, производимых ветром на пластинку перпендикулярно ее плоскости (рис. 2.4, а).
25
|
|
Решение.Рассмотрим равновесие пластинки. Отбросим шарнир О. Так как пластинка однородная и прямоугольной формы, то равнодействующая Р давлений ветра и сила тяжести G пересекаются в геометрическом центре С пластинки; линия действия реакции R0 шарнира на основании теоремы о равновесии трех непараллельных сил также пройдет через точку С. Для системы трех сходящихся сил, действующих на пластинку, применим аналитическое условие равновесия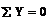 
, направив ось у перпендикулярно пластинке (чтобы реакция R0, которую не требуется определять, не вошла в уравнение равновесия). Составим уравнение равновесия
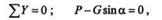
откуда
|
|
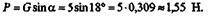
| Построим замкнутый силовой треугольник (рис. 2.4, б). Решая его, получаем |
|
|
Проведем проверку решения задачи с помощью геометрического условия равновесия:
Глава 3
Дата добавления: 2018-04-15; просмотров: 981; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!