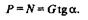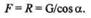ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
Геометрический способ определения
Равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема.Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
|
|
| Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3: |
|
|
| где F |
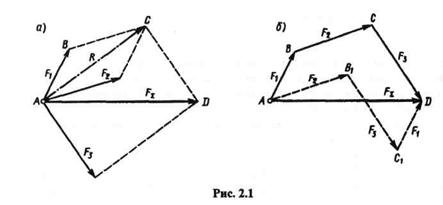
Пусть дана плоская система трех сил F1, F2 и F3, линии действия которых сходятся в точке А. На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А.Сложив первые две силы F1 и F2 по правилу параллелограмма, получим их равнодействующую R (рис. 2.1, a):
|
|
|
|
|
|
| Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим |
| Сокращенно это равенство запишем так: |
где i — все целые числа от 1 до n, а греческая заглавная буква 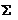 (сигма) означает сумму.
(сигма) означает сумму.
Очевидно, что построение, выполненное на рис. 2.1, а, можно заменить более простым (рис. 2.1, б). Многоугольник ABCD называется силовым многоугольником. Сторона AD,соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (рис. 2.1, б).
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется (рис. 2.1, б,многоугольник AB1C1D).
20
Геометрическое условие равновесия
Плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая F 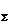 системы сходящихся сил,
системы сходящихся сил,
дающих замкнутый силовой многоугольник, равна нулю и, следовательно, эта система эквивалентна нулю, т. е. находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством
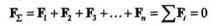
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины,называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
1) выбирают тело, равновесие которого будет рассматриваться;
2) отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
3) пользуясь условиями равновесия, находят неизвестные величины.
При решении задач технической механики необходимо строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
Пользуясь этим правилом, целесообразно в сомнительных случаях проверять правильность хода решения задач, для чего следует поставить в слагаемые проверяемого равенства единицы всех входящих в него величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Проверим таким способом приведенную в § 1.6 формулу Q = ql:
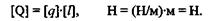
Единицы правой и левой частей равенства одинаковы, следовательно, формула по размерности верна.
Следует заметить, что такая проверка ничего не говорит о правильности нередко входящих в формулы числовых коэффициентов.
21
|
|
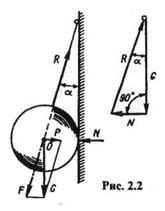
Пример 2.1. К вертикальной гладкой стене на веревке, составляющей со стеной угол а, подвешен однородный шар (рис. 2.2). Определить натяжение веревки F и силу давления шара Р на стену, если сила тяжести шара G.
Решение. Рассмотрим равновесие шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара. Так как шар однородный, то сила тяжести G приложена в его геометрическом центре. Реакция Rнаправлена вдоль веревки и, согласно теореме о равновесии трех непараллельных сил, ее линия действия также должна проходить через центр шара. Ксистеме трех сходящихся сил, приложенных к шару, применим геометрическое условие равновесия:
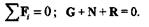
Строим замкнутый силовой многоугольник, начиная с изображения в произвольном масштабе вектора известной силы G.
Направление обхода треугольника (т. е. направление стрелок) определяется этой силой. Решая треугольник, получим
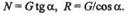
|
|
| Натяжение F веревки по модулю равно ее реакции R: |
|
|
Искомая сила давления Р шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции Nстены, но направлена в противоположную сторону:
Эту же задачу можно решить, разложив силу тяжести G по реальным направлениям (направлениям реакций) на составляющие Р (сила давления шара на стену) и F (натяжение веревки), причем, согласно аксиоме взаимодействия, F = R, Р = N.
Из построенного параллелограмма (рис. 2.2) легко определяем искомые величины. Такой метод решения задачи называют методом разложения.
Дата добавления: 2018-04-15; просмотров: 1669; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

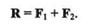
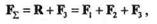
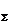 — равнодействующая данной системы трех сил.
— равнодействующая данной системы трех сил.