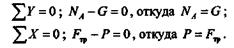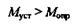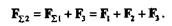Устойчивость против опрокидывания
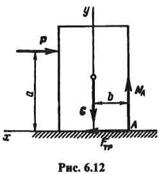
Рассмотрим твердое тело весом G, опирающееся на плоскость и способное опрокидываться вокруг какого-то ребра под действием горизонтальной силы Р (рис. 6.12). Допустим, что силы Ри G лежат в одной плоскости, пересекающейся с ребром в точке А. В момент начала опрокидывания на тело будут действовать также нормальная реакция NA и сила трения Ftp, приложенные в точке А,причем в случае равновесия системы всех четырех сил можно записать два уравнения равновесия:
|
|
Таким образом, в момент начала опрокидывания на рассматриваемое тело действуют пара сил (Р, Fтр), стремящаяся опрокинуть тело, и пара сил (G, NА), противодействующая опрокидыванию.
Очевидно, что опрокидывания не произойдет, если
|
|
M(G,NA) > M(P, Fтр) или Gb > Pa.
Произведение Gb равно моменту силы G относительно точки А и называется моментом устойчивости. Момент силы Р относительно той же точки, равный произведению Ра, называется опрокидывающим моментом.
|
|
| и сформулируется так: для устойчивости |
Условие устойчивости против опрокидывания запишется в виде неравенства
56
твердого тела против опрокидывания необходимо и достаточно, чтобы момент устойчивости был больше опрокидывающего момента.
Если на тело действуют несколько сил, стремящихся его опрокинуть, то опрокидывающий момент равен сумме моментов этих сил относительно точки, вокруг которой может произойти опрокидывание. То же относится и к моменту устойчивости.
Отношение момента устойчивости к опрокидывающему моменту называется коэффициентом устойчивости:
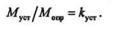
Очевидно, что в сооружениях должно быть kуст > 1.
Расчет на устойчивость особенно важен для высоких сооружений, таких, как дымовые трубы, мачты, краны, высокие стены и т. п. Заметим, что в случае, когда Р > Fтр,а опрокидывающий момент меньше момента устойчивости, тело будет скользить по опорной плоскости, конечно, если конструкция допускает такое движение.
Глава 7
ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
Пространственная система сходящихся сил
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил.
Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной тЪчке.
Теорема. Пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система п сходящихся сил (F1, F2, F3 ..., Fn). На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма сложим силы F1 и F2, в результате чего получим их равнодействующую:
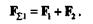
Сложив эту равнодействующую с силой F3, получим равнодействующую трех сил:
57
|
|
Повторив указанную операцию п - 1 раз, получим равнодействующую системы п сил, которая будет равна векторной сумме этих сил; линия действия равнодействующей будет проходить через точку пересечения линий действия составляющих:
|
|
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей неприемлемы, а применяется аналитический способ (методпроекций).
Дата добавления: 2018-04-15; просмотров: 1917; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!