Содержание лабораторной работы.

1. Ввести выборочные данные.

2. Построить корреляционную матрицу.

3. Оценить параметры уравнения множественной линейной регрессии.

4. Проверить значимость коэффициентов уравнения регрессии и самого уравнения регрессии при уровне значимости .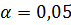

5. Оценить качество построенной модели.

6. Построить точечный и интервальный, надежности 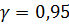, прогнозы среднего зависимой переменной для значений факторов равных их выборочным средним, т.е. для .

7. Дать общее заключение об оцененной модели и ее интерпретацию.

Выполнение работы в MSExcel.

Порядок выполнения работы рассмотрим на примере построения линейной регрессионной зависимости расходов на жилье (Y, млрд. дол.) от располагаемого личного дохода (X, млрд. дол.) и индекса реальных цен (Р) относительно 1972 г. по данным США за 1959–1978 г. Эти данные приведены на рис.6.1.

Ввод данных.В ячейках A1-А21 расположим имя фактора Х (располагаемый личный доход) и его значения, в ячейках B1-В21 имя фактора Р (индекса реальных цен) и его значения, в ячейках C1-С21 имя зависимой переменной Y (расходы на жилье) и его значения.

Построение корреляционной матрицы. Следуя работе №2, построим корреляционную матрицу для величин X, P, Y. Расположим ее в ячейках G5-I7, см. рис. 6.1. Парные коэффициенты корреляции , , говорят о тесной парной линейной корреляционной зависимости рассматриваемых величин.

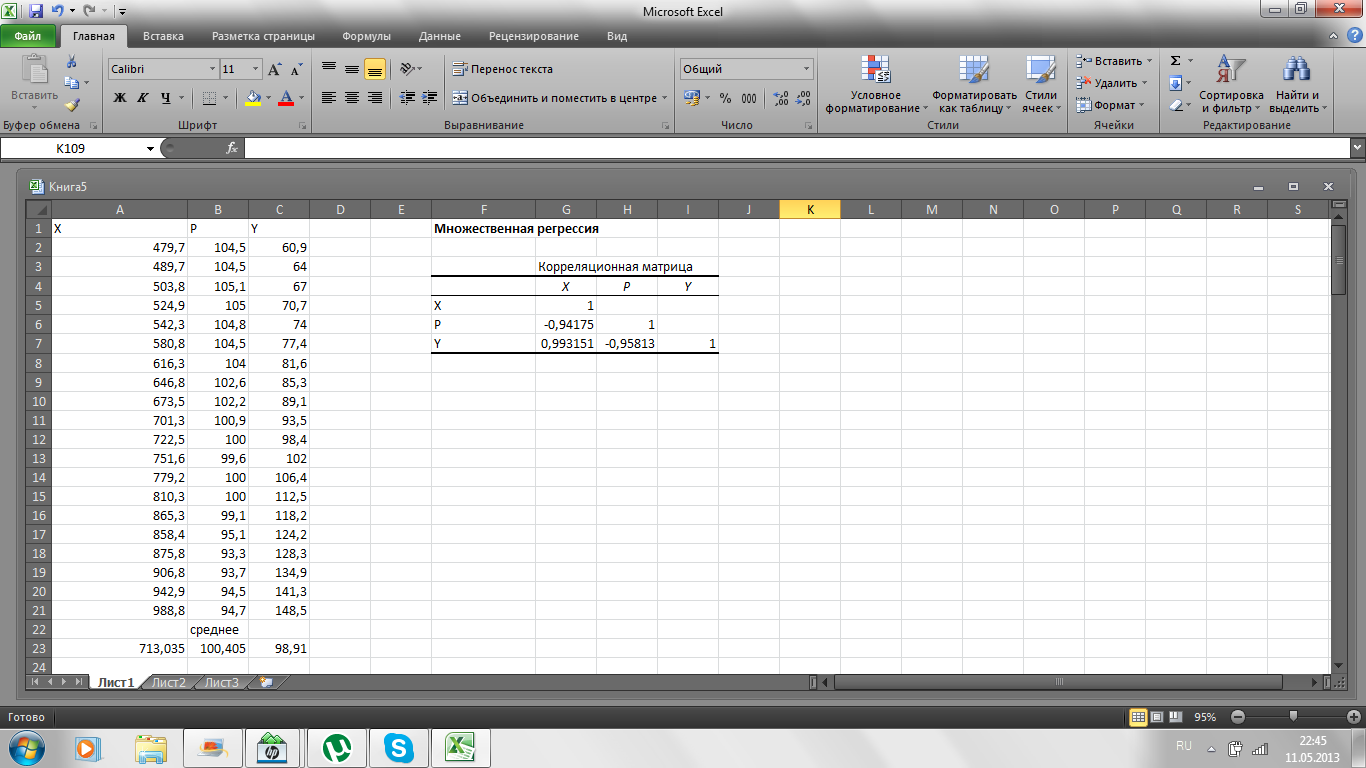
Рис. 6.1. Множественная регрессия

Оценка уравнения множественной линейной регрессии .Откроем вкладку «Данные», в группе «Анализ» выберем надстройку «Анализ данных». В открывшемся окне «Инструменты анализа» выберем функцию «Регрессия». В появившемся окне «Регрессия» укажем входные данные для оценки параметров уравнения регрессии, выводимые результаты и их расположение. Заполнение окна «Регрессия» для рассматриваемого примера приведено на рис. 6.2. В части «Входные данные» в поле ввода «Входной интервал Y» указываем диапазон ячеек, содержащий значения зависимой переменной, в нашем примере это С1:С21. В поле ввода «Входной интервал X» – диапазон ячеек, содержащий значения независимых переменных, в примере это A1:В21. Значения объясняющих переменных должны располагаться в последовательных столбцах. В поле «Метки» устанавливаем флажок , он указывает на то, что первые строки диапазонов данных содержат имена этих данных (заголовки). В «Константа-ноль» флажок не устанавливаем. При установке флажка в левом поле «Уровень надежности», наряду с используемым по умолчанию стандартным уровнем надежности 95% ( 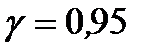), можно задать и другое его значение, в этом случае будут выведены интервальные оценки параметров регрессии для двух уровней надежности.

В части «Параметры вывода» выбираем «Выходной интервал» – для помещения результатов на текущем рабочем листе, положение результатов на листе указываем заданием верхней левой ячейки, начиная с которой располагаются результаты, внашем примере выбрана ячейка А25.Далее, выставляя флажки, указываем какую дополнительную информацию, предлагаемую функцией «Регрессия», мы хотим иметь в результатах:

· «Остатки» – для выдачи прогнозов и остатков регрессии ;

· «График остатков» – для вывода точечной диаграммы остатков ;

· «График подбора» – для вывода наложенных на диаграмму рассеяния точек линии регрессии. По «ОК»получаем результаты регрессии, которые включают в себя таблицу регрессионной статистики, таблицу дисперсионного анализа, таблицу коэффициентов регрессии, таблицу остатков и графики остатков и подбора. Результаты регрессии приведены на рис. 6.3 – 6.4.Пояснения к выводимым результатам см. в работе № 4.

Рис. 6.2. Заполнение окна «Регрессия»

Рис. 6.3. Итоги регрессии

Из таблицы коэффициентов регрессии имеем следующие МНК-оценки параметров уравнения регрессии , , . Их стандартные ошибки равны . 95%-е доверительные интервалы коэффициентов регрессии: ; ; . В таблице «Регрессионная статистика» величина «Стандартная ошибка» является оценкой стандартного отклонения зависимой переменной (ошибки регрессии), т.е. .

Построенное уравнение регрессии: .

Рис. 6.4. Графики остатков и подбора множественной регрессии

Графики остатков и подбора в множественной регрессии в MSExcel выдаются отдельно по каждому фактору. Приведенные на рис. 6.4 графики остатков регрессии имеют колебательный характер, а графики подбора говорят о хорошем качестве подгонки построенной модели к наблюдаемым данным.

Верификация модели. Проверка значимости коэффициентов уравнения регрессии (значимого влияния располагаемого личного дохода Xи индекса реальных цен Pна совокупные расходы на жилье Y) путем проверки нулевых гипотез с помощью t-статистик .Для вычислениякритического значения при n=20, р=3 и 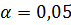выделим ячейку G45, в вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «СТЬЮДЕНТ.ОБР.2Х». В окне этой функции в поле «Вероятность» введем значение , равное 0,05, в поле «Степени свободы» зададим число степенейn-p, равное 17. По «ОК» в ячейке G45 получим значение , в рассматриваемом примере оно равно 2,1098 (см. рис. 6.3).Значения t-статистик для коэффициентов уравнения регрессии соответственноравны и превышают по модулю критическое значение . Следовательно, при уровне значимости 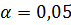коэффициенты уравнения регрессии значимо отличаются от нуля. О значимом влиянии располагаемого личного дохода X и индекса реальных цен Р на расходы на жилье Y говорят также р-значения, которые меньше заданного уровня значимости 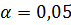, а также доверительные интервалы для коэффициентов уравнения регрессии, которые не содержат нуля.

Большие значения скорректированного коэффициента детерминации и F-статистики, , уровень значимости (Значимость F)которой 4,248*10^-18 существенно меньше заданного уровня значимости 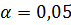,говорят о статистической значимости построенного уравнения регрессии и хорошем качестве подгонки модели к выборочным данным. 98,99% вариации зависимой переменной объясняется вариацией объясняющих переменных.

Построение точечного и интервального прогнозы среднего зависимой переменной. Построение прогноза среднего зависимой переменной для значений факторов равных их выборочным средним, т.е. для . Для нахождения выборочных средних факторов и зависимой переменной последовательно выделяя, например, ячейки А23, В23, С23 и вводя соответственно в строке формул =СРЗНАЧ(А2:А21),=СРЗНАЧ(В2:В21),=СРЗНАЧ(С2:С21), получим значения выборочных средних , , . Для вычисления прогноза среднего при заданных значениях факторов выделим, например, ячейку Н102 и, учитывая расположение значений факторов и коэффициентов уравнения регрессии, в строке формул введем =В41+В42*А23+В43*В23. По ОК в Н102получим искомое значение , совпадающее с выборочным средним , см. рис. 6.5.

Построение интервальной оценки среднего зависимой величины надежности 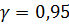. Доверительный интервал надежности 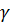для среднего 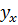зависимой величины при заданном векторе значений факторов определяется неравенством

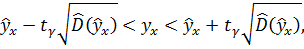
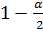где – квантиль уровня распределения Стьюдента с числом степеней свободы . Оценка дисперсии прогноза для заданного вектора значений факторов определяется как . Предварительно вычислим оценку дисперсии прогноза (см. рис. 6.5).

Для этого в ячейках А100-С119 создадим матрицу X, первый столбец которой состоит из единиц, второй – из значений фактора Х, третий – из значений фактора Р. В ячейках В123-U125разместим транспонированную матрицу . В ячейках F98-H98 расположим вектор ( )=(1;713,035;100,405) значений факторов для которых вычисляется интервальный прогноз. В ячейках K98-K100 расположим транспонированный вектор . Выделим ячейку Н105 и, учитывая расположение величины sв ячейке В31, в строке формул введем

=B31^2*(1+МУМНОЖ(МУМНОЖ(F98:H98;МОБР(МУМНОЖ(B123:U125;A100:C119)));K98:K100)). По «Enter» в этой ячейке получим искомое значение оценки дисперсии среднего, равное 7,734. Выделим под нижнюю границу доверительного интервала ячейку К108и в строке формул введем

=H102-СТЬЮДЕНТ.ОБР(0,975;17)*КОРЕНЬ(H105)

По Enter в ячейке К108 получим значение нижней границы доверительного интервала, равное 93,0426. Аналогично, выделив ячейку N108 и введя в строке формул

=H102+СТЬЮДЕНТ.ОБР(0,975;17)*КОРЕНЬ(H105),

получим в ней значение верхней границы доверительного интервала, равное 104,777.Таким образом, доверительный интервал, надежности для среднего 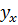зависимой величиныY(расходов на жилье) для значений факторов 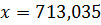иp задается неравенством

Рис. 6.5. Построение точечного и интервального прогноза среднего

Общее заключение об оцененной модели и ее интерпретация.

Построенная модель линейной множественной регрессии средних расходов на жилье Y (млрд. дол.)от располагаемого личного дохода X(млрд. дол.) и индекса реальных ценP (%)

хорошо согласуется с имеющейся выборкой. Об этом свидетельствует высокое значение нормированного коэффициента детерминации , т.е. 98,99% вариации Y относительной ее средней объясняется изменениями X иP. Большое значение -статистики, , и ее уровень значимости, равный , свидетельствует о наличии значимой линейной корреляционной зависимости Y отX иP. Оценка среднеквадратического отклонения ошибок регрессии мала по сравнению с , что также свидетельствует о малом разбросе выборочных данных относительно плоскости регрессии. Значения t-статистик коэффициентов уравнения регрессии и их p-значения, равные соответственно 0,0197, и 0,00091 говорят об их значимом отличии от нуля. Следовательно, располагаемый личный доход и индекс цен значимо влияют на расходы на жилье и построенная регрессионная модель статистически значима.

Интерпретация построенной модели . Коэффициент при индексе цен p имеет отрицательный знак, что согласуется с теоретическим положением о снижении спроса на жилье с ростом цен. Коэффициент при величине располагаемых доходовxположительный, что согласуется с положением о росте спроса с ростом доходов. Значения коэффициентов при xи p говорят о возрастании расходов на жилье в среднем на 0,13388 млрд. дол при росте располагаемых личных доходов на 1млрд. дол. и сокращении расходов на жилье на 1,31194 млрд. дол при росте индекса цен на 1%.

Выборочный коэффициент корреляции располагаемого личного дохода Х и индекса цен Р близок по модулю к единице, , это говорит о сильной коррелированности рассматриваемых факторов и о необходимости проведения дополнительных исследований на мультиколлинеарность. Кроме того, выборочные данные являются временными рядами, поэтому возможна автокорреляции остатков. Следовательно, необходимо исследовать построенную модель на автокорреляцию остатков.

Контрольные вопросы.

1. В чем заключается спецификация модели множественной регрессии?

2. Что характеризуетмножественный коэффициент корреляции?

3. Как находятся оценки параметров линейной множественной регрессии?

4. Может ли быть линейная множественная регрессия быть нелинейной по объясняющим переменным?

5. Сформулируйте критерии значимости параметров множественной регрессии.

6. Приведите предпосылки линейной множественной регрессии.

7. Сформулируйте Теорему Гаусса-Маркова.

8. С помощью каких критериев проверяется значимость линейного уравнения множественной регрессии?

9. В чем отличие ошибок регрессии от остатков регрессии?

10. Что характеризует скорректированный коэффициент детерминации?

11. Как определяется средняя ошибка аппроксимации, что она характеризует?

12. Как интерпретируются коэффициенты линейной множественной регрессии?

13. Что характеризует частный коэффициент эластичности для линейной множественной регрессии?

14. В чем заключается прогноз значений зависимой переменной? Как определяется дисперсия прогноза?

15. Как строится интервальный прогноз среднего зависимой переменной?

16. С увеличением надежности интервального прогноза он увеличивается или уменьшается?

Лабораторная работа № 7. Анализ мультиколлинеарности и авторегрессии
в модели множественной регрессии

Цель работы. Освоение методов выявления мультиколлинеарности и автокорреляции ошибок в множественной регрессии с использованием пакета анализа MSExcel 2010.

Краткие сведения. Здесь используются обозначения, принятые в кратких сведениях к лабораторной работе №6.

Мультиколлинеарность.

Одной из предпосылок классической линейной регрессии является предположение о линейной независимости объясняющих переменных. Это означает линейную независимость векторов-столбцов , ,…, значений факторов, что равносильно тому, что определитель матрицы не равен нулю (ранг этой матрицы и матрицы Xравен p). В этом случае существует обратная матрица и оценки коэффициентов уравнения регрессии однозначно определяются соотношением

Под мультиколлинеарностью понимается высокая взаимная коррелированность факторов, выбранных в качестве объясняющих переменных в модели множественной регрессии. Мультиколлинеарность может проявляться в функциональной (полной, явной) и стохастических формах.

При функциональнойформе мультиколлинеарности между факторами (между векторами-столбцами , ,…, значений факторов) существует линейная функциональная зависимость, т.е. нарушается предположение о линейной независимости объясняющих переменных. В этом случае определители матрицы и матрицы 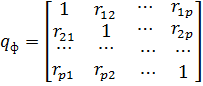выборочных коэффициентов корреляции между факторами , ,…, равны нулю, что не позволяет получить однозначные оценки коэффициентов уравнения регрессии.Если факторы линейно независимы, то и . Если хотя бы два фактора линейно зависимы, например, , то и .

В стохастической форме мультиколлинеарности между хотя бы двумя объясняющими переменными существует тесная линейная корреляционная зависимость. В этом случае определитель матрицы отличен от нуля, но может принимать очень маленькие по модулю значения, а и близок к нулю. Это приводит к большим значениям элементов обратной матрицы . Следовательно, оценки дисперсий коэффициентов регрессии принимают большие значения и не имеют смысла, в силу малости вычисленных значений t-статистик коэффициентов регрессии. Кроме того, в этом случае вычислительные погрешности приводят к значительным ошибкам в оценках коэффициентов регрессии и их дисперсий. При этом уравнение линейной множественной регрессии может оказаться в целом значимым по F-критерию при незначимости некоторых коэффициентов уравнения регрессии. Стохастическая форма мультиколлинеарности факторов частое явление в экономических исследованиях.

Точных количественных критериев выявления наличия или отсутствия мультиколлинеарности в стохастической форме не существует. Для выявления мультиколлинеарности используют его следующие характерные признаки.

· Анализ корреляционной матрицы. Если модули некоторых парных коэффициентов корреляции между факторами превышает 0,75, то имеет место мультиколлинеарность.

· Определители матрицы ,выборочных коэффициентов корреляции между факторами,близок к нулю.

· Небольшие изменения выборочных данных (например, отбрасывание небольшой части выборочных данных или добавление небольшого количества новых данных) приводят к существенному изменению оценок коэффициентов уравнения регрессии.

· Оценки коэффициентов уравнения регрессии имеют большие стандартные отклонения и малую значимость, а само уравнение в целом значимо, о чем свидетельствуют большие значения коэффициента детерминации и F-статистики.

· Интерпретация коэффициентов уравнения регрессии не согласуется с положениями экономической теории (например, коэффициенты имеют знаки или значения, не согласующиеся с теорией).

Наличие мультиколлинеарности требует доработки модели с целью ее устранения или уменьшения. Эти методы рассматриваются в более широких курсах эконометрики.

Автокорреляция ошибок регрессии.

При построении регрессионных моделей по временным рядам (упорядоченным данным за последовательные моменты или промежутки времени) предположение о некоррелированности ошибок регрессии и (или и ) в разных наблюдениях не выполняется, т.е. . Это объясняется тем, что значения изучаемых величин в момент времени t в значительной степени зависят от их значений в предшествующие моменты времени. В этом случае говорят об автокорреляции данных и строят авторегрессионные модели, учитывающие автокорреляцию данных. Простейшим примером такой модели является авторегрессионный процесс первого порядка: , который описывает ошибку регрессии в момент времени tкак линейную функцию от ошибки в момент времени t-1 и случайной ошибки 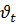распределенной по нормальному закону с нулевым средним и постоянной дисперсией для всех t. Величина называется коэффициентом авторегрессии. Авторегрессионные модели рассматриваются в более подробных курсах эконометрики.

Применение метода наименьших квадратов для оценивания множественной регрессии 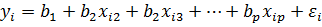при наличии корреляции ошибок дает несмещенные и состоятельные оценки коэффициентов регрессии, но оценки их дисперсий несостоятельные и смещенные (как правило, в сторону занижения). Это приводит к тому, что результаты тестирования гипотез о значимости коэффициентов регрессии по t-критерию оказываются недостоверными и оцененная модель дает более оптимистическую картину регрессии, чем есть на самом деле.

Различают положительную автокорреляцию при положительном коэффициенте авторегрессии , что геометрически выражается в чередовании зон с положительными и отрицательными значениями остатков регрессии . Отрицательная автокорреляцияимеет место при отрицательном коэффициенте авторегрессии , что геометрически выражается в том, что последовательные значения остатков регрессии имеют разные знаки. Таким образом, о наличии автокорреляции можно судить по графику остатков.

Для выявления наличия автокорреляции первого порядка (зависимости значения только от предшествующего значения ) используется критерий Дарбина-Уотсона. Этот критерий основан на простой идеи: если корреляция есть в ошибках регрессии , то она присутствует и в остатках регрессии 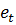получаемых после применения метода наименьших квадратов. Критерий Дарбина-Уотсона основан на статистике

которая принимает значения от 0 до 4. Нулевая гипотеза об отсутствии автокорреляции (Н₀: ) принимается или отклоняется при попадании наблюдаемого (вычисленного) значения dв промежутки в соответствии с рис. 7.1.

Н₀отвергается, положительная автокорреляция	Зона неопределенности	Н₀ принимается, автокорреляция отсутствует	Зона неопределенности	Н₀отвергается, отрицательная автокорреляция
0	d_н	d_в	4-d_в	4-d_н 4

Рис. 7.1. Критерий Дарбина-Уотсона

При автокорреляция отсутствует; при или ничего о наличии или отсутствии автокорреляции сказать нельзя (зона неопределенности критерия); при нулевая гипотеза отвергается и имеет место положительная автокорреляция; при нулевая гипотеза отвергается и имеет место отрицательная автокорреляция. Верхние и нижние границы критического значения статистики критерия Дарбина-Уотсона для уровня значимости 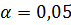приводятся в специальных таблицах, например, в приложении 2.4 учебника Эконометрика / И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др.

Дата добавления: 2018-04-15; просмотров: 706; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!