Лабораторная работа № 4. Парная линейная регрессия
Цель работы. Освоение построения по выборочным данным модели парной линейной регрессии, оценки точности и надежности параметров и всей модели, построения прогнозов значений зависимой переменной в MSExcel 2010. Интерпретация модели.
Краткие сведения. Модель парной линейной регрессии описывает зависимость условного среднего  зависимой случайной величины
зависимой случайной величины  в виде линейной функции значений
в виде линейной функции значений 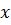 объясняющей переменной (фактора)
объясняющей переменной (фактора) 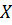 :
:  . Наблюдаемые в выборке
. Наблюдаемые в выборке  значения
значения  зависимой переменной
зависимой переменной  описываются в виде суммы детерминированной
описываются в виде суммы детерминированной  и случайной
и случайной  составляющих:
составляющих:
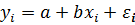 . (4.1)
. (4.1)
Случайная величина  , называемая ошибкой регрессии, отражает влияние пропущенных объясняющих переменных, неправильной структуры и функциональной спецификации модели, агрегирования переменных, ошибки измерений.
, называемая ошибкой регрессии, отражает влияние пропущенных объясняющих переменных, неправильной структуры и функциональной спецификации модели, агрегирования переменных, ошибки измерений.
Основные предпосылки парной линейной регрессии.
1. Связь значений зависимой величины от значений фактора задается соотношением (4) (эта зависимость называется спецификацией модели).
2.  – детерминированные величины, линейно не связанные между собой, т.е. векторы
– детерминированные величины, линейно не связанные между собой, т.е. векторы  и (1, 1, …, 1) не коллинеарные.
и (1, 1, …, 1) не коллинеарные.
3. Ошибки регрессии  – случайные величины с
– случайные величины с  для всех
для всех  .
.
4. Ошибки регрессии  и
и  (или переменные
(или переменные  и
и  ) не коррелированы в разных наблюдениях, т.е.
) не коррелированы в разных наблюдениях, т.е.  .
.
5. Ошибки регрессии  распределены по нормальному закону с нулевой средней и дисперсией
распределены по нормальному закону с нулевой средней и дисперсией 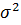 , т.е.
, т.е. 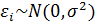 , соответственно
, соответственно  .
.
|
|
|
Модель парной линейной регрессии содержит три неизвестных параметра: коэффициенты  и
и 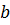 уравнения регрессии и дисперсию
уравнения регрессии и дисперсию 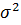 ошибок регрессии
ошибок регрессии  . Оценки коэффициентов
. Оценки коэффициентов  и
и 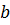 находятся из условия минимизации по
находятся из условия минимизации по  и
и 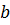 суммы квадратов
суммы квадратов

отклонений наблюдаемых значений  от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии 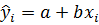 . Эти оценки называются оценками метода наименьших квадратов и определяются соотношениями
. Эти оценки называются оценками метода наименьших квадратов и определяются соотношениями
 ,
,  ,
,
где  – выборочная ковариация величин
– выборочная ковариация величин 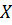 и
и  ,
,  – выборочная дисперсия
– выборочная дисперсия 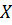 ,
,  и
и  – выборочные среднеквадратические отклонения величин X и Y,
– выборочные среднеквадратические отклонения величин X и Y,  и
и 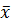 – выборочные средние
– выборочные средние  и
и 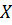 .
.
Согласно теоремы Гаусса-Маркова, при выполнении предпосылок 1–4, эти оценки обладают наименьшей дисперсией в классе всех линейных несмещенных оценок.
Величины  называются остатками регрессии.
называются остатками регрессии.
Несмещенной оценкой дисперсии 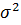 ошибок регрессии
ошибок регрессии  является величина
является величина
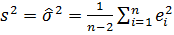 .
.
Оценки дисперсий оценок  и
и  определяются как
определяются как
 ,
,  .
.
Стандартные отклонения коэффициентов уравнения регрессии определяются соотношениями  и
и  .
.
Интервальные оценки параметров уравнения регрессии надежности 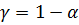 :
:
 ,
,
 ,
,
 (4.2)
(4.2)
где 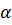 заданный уровень значимости,
заданный уровень значимости,  – квантиль уровня
– квантиль уровня 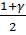 распределения Стьюдента (
распределения Стьюдента (  -распределения) с числом степеней свободы
-распределения) с числом степеней свободы  ,
,  и
и 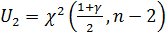 –квантили соответственно уровней
–квантили соответственно уровней 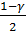 и
и 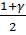 распределения
распределения 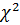 с числом степеней свободы
с числом степеней свободы  .
.
|
|
|
Оцененное уравнение регрессии  на
на 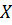 имеет вид
имеет вид  . Статистическая значимость параметров уравнения регрессии (их значимое отличие от нуля) определяется путем проверки принадлежности нулевых значений доверительным интервалам. Если доверительный интервал надежности
. Статистическая значимость параметров уравнения регрессии (их значимое отличие от нуля) определяется путем проверки принадлежности нулевых значений доверительным интервалам. Если доверительный интервал надежности 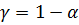 содержит ноль, то нулевая гипотеза о равенстве параметра нулю принимается с уровнем значимости
содержит ноль, то нулевая гипотеза о равенстве параметра нулю принимается с уровнем значимости 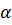 . Проверка значимого отличия от нуля параметров
. Проверка значимого отличия от нуля параметров  и
и 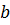 уравнения регрессии осуществляетсятакжепутем проверки нулевых гипотез
уравнения регрессии осуществляетсятакжепутем проверки нулевых гипотез  и
и  против альтернативных гипотез
против альтернативных гипотез 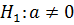 и
и  . Для проверки этих гипотез используются
. Для проверки этих гипотез используются  - статистики
- статистики  и
и  , распределенные по закону Стьюдента с
, распределенные по закону Стьюдента с 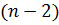 степенями свободы. Если вычисленные значения статистик
степенями свободы. Если вычисленные значения статистик  или
или  превышают по модулю критическое значение
превышают по модулю критическое значение  , то нулевая гипотеза отвергается и принимается альтернативная гипотеза (параметр значимо отличается от нуля). Если вычисленное значения
, то нулевая гипотеза отвергается и принимается альтернативная гипотеза (параметр значимо отличается от нуля). Если вычисленное значения  - статистики по модулю меньше критического значения
- статистики по модулю меньше критического значения  , то нулевая гипотеза принимается (параметр незначимо отличается от нуля) при заданном уровне
, то нулевая гипотеза принимается (параметр незначимо отличается от нуля) при заданном уровне 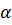 .Критическое значение
.Критическое значение  определяется как квантиль уровня
определяется как квантиль уровня  распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  .Принятие нулевой гипотезы
.Принятие нулевой гипотезы  говорит об отсутствии значимой линейной корреляционной зависимости величин Y и X.
говорит об отсутствии значимой линейной корреляционной зависимости величин Y и X.
|
|
|
Верификация и оценка качества модели. Верификация модели парной линейной регрессии означает проверку соответствия модели эмпирическим данным и заключается в установлении значимости уравнения регрессии, т.е. в значимости влияния фактора 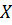 на условную среднюю зависимой величины
на условную среднюю зависимой величины  . Проверка значимости уравнения регрессии заключается в проверке нулевой гипотезы
. Проверка значимости уравнения регрессии заключается в проверке нулевой гипотезы  , об отсутствии влияния фактора
, об отсутствии влияния фактора 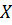 на зависимую величину
на зависимую величину  , против альтернативной гипотезы
, против альтернативной гипотезы  , о значимом влиянии фактора
, о значимом влиянии фактора 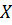 на
на  . Значимость уравнения регрессии может быть проверена двумя равноценными способами: с использованием дисперсионного анализа; с использование теории корреляции.
. Значимость уравнения регрессии может быть проверена двумя равноценными способами: с использованием дисперсионного анализа; с использование теории корреляции.
Дисперсионный анализ в линейной регрессии основывается на том, что общая сумма квадратов отклонений  от их общего среднего
от их общего среднего  ,
,  , разлагается на сумму квадратов отклонений, объясняемых регрессией,
, разлагается на сумму квадратов отклонений, объясняемых регрессией,  , и остаточную сумму квадратов отклонений
, и остаточную сумму квадратов отклонений  . При справедливости нулевой гипотезы
. При справедливости нулевой гипотезы  средние квадраты
средние квадраты 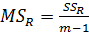 и
и  являются независимыми несмещенными оценками одной и той же генеральной дисперсии
являются независимыми несмещенными оценками одной и той же генеральной дисперсии 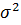 зависимой переменной
зависимой переменной  и их различие незначимо. Проверка нулевой гипотезы
и их различие незначимо. Проверка нулевой гипотезы  , при уровне значимости
, при уровне значимости 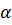 , сводится к проверке существенности различия несмещенных выборочных оценок
, сводится к проверке существенности различия несмещенных выборочных оценок 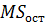 и
и 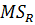 дисперсии
дисперсии 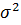 с помощью F-критерия
с помощью F-критерия  , который имеет F-распределение Фишера-Снедекора с
, который имеет F-распределение Фишера-Снедекора с 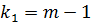 и
и  степенями свободы, где
степенями свободы, где 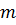 число коэффициентов в уравнении регрессии, а n объем выборки. Гипотеза
число коэффициентов в уравнении регрессии, а n объем выборки. Гипотеза 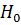 об отсутствии влияния фактора
об отсутствии влияния фактора 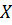 на исследуемый признак
на исследуемый признак  принимается, если вычисленное значение статистики
принимается, если вычисленное значение статистики  меньше критического
меньше критического  . Если
. Если  , то гипотеза
, то гипотеза 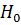 отвергается и принимается гипотеза
отвергается и принимается гипотеза  , т.е. фактор
, т.е. фактор 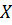 оказывает влияние на исследуемый признак
оказывает влияние на исследуемый признак  .
.  – квантиль уровня
– квантиль уровня 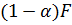 -распределения Фишера-Снедекора с
-распределения Фишера-Снедекора с 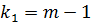 и
и  степенями свободы.
степенями свободы.
|
|
|
Использование элементов теории корреляции при проверке значимости уравнения регрессии основано на соотношении  и заключается в проверке значимого отличия от нуля коэффициента корреляции
и заключается в проверке значимого отличия от нуля коэффициента корреляции 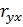 , следовательно, и значимости коэффициента регрессии
, следовательно, и значимости коэффициента регрессии 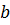 . Проверка нулевой гипотезы
. Проверка нулевой гипотезы 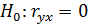 , т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X, производится с помощью статистики
, т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X, производится с помощью статистики  , которая при справедливости нулевой гипотезы имеет распределение Стьюдента (t-распределение) с числом степеней свободы
, которая при справедливости нулевой гипотезы имеет распределение Стьюдента (t-распределение) с числом степеней свободы  . Гипотеза
. Гипотеза 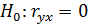 отвергается при уровне значимости
отвергается при уровне значимости 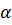 (т.е. оцененное уравнение линейной регрессии значимо), если вычисленное по выборке объема
(т.е. оцененное уравнение линейной регрессии значимо), если вычисленное по выборке объема  значениеt-статистики удовлетворяет неравенству
значениеt-статистики удовлетворяет неравенству
 , (4.3)
, (4.3)
где  – квантиль уровня
– квантиль уровня  распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  . Если нулевая гипотеза
. Если нулевая гипотеза 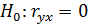 принимается, то оцененное уравнение линейной регрессии незначимо – зависимая величина Y и фактор
принимается, то оцененное уравнение линейной регрессии незначимо – зависимая величина Y и фактор 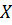 не связаны линейной корреляционной зависимостью.
не связаны линейной корреляционной зависимостью.
Для парной линейной регрессии оба способа проверки значимости уравнения регрессии равнозначны, а F-критерий и t-критерий связаны равенством  .
.
Мерой качества уравнения регрессии и характеристикой прогностической силы регрессионной модели является коэффициент детерминации
 ,
,
который показывает, какая доля вариации зависимой переменной объясняется вариацией фактора.  . Значимое отличие от нуля коэффициента детерминации
. Значимое отличие от нуля коэффициента детерминации  устанавливается также с помощью приведенного выше F-критерия. F-критерий и коэффициент детерминации
устанавливается также с помощью приведенного выше F-критерия. F-критерий и коэффициент детерминации  связаны равенством
связаны равенством  .Для парной линейной регрессии коэффициент детерминации
.Для парной линейной регрессии коэффициент детерминации  .
.
Качество подгонки построенной линейной регрессии к выборочным данным характеризуется средней ошибкой аппроксимации
 .
.
Прогнозирование по уравнению регрессии. Точечный прогноз  среднего зависимой величины
среднего зависимой величины  для заданного значения
для заданного значения 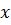 вычисляется по уравнению регрессии
вычисляется по уравнению регрессии  и является наилучшей несмещенной линейной оценкой теоретического условного среднего
и является наилучшей несмещенной линейной оценкой теоретического условного среднего  . Доверительный интервал надежности
. Доверительный интервал надежности 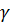 прогноза условного среднего для заданного значения
прогноза условного среднего для заданного значения 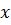 задается неравенством
задается неравенством
 (4.4)
(4.4)
Здесь  – квантиль уровня
– квантиль уровня 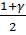 распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  ,
,  – оценка дисперсии прогноза условного среднего величины Y,
– оценка дисперсии прогноза условного среднего величины Y,  – выборочная дисперсия независимой переменной X. Графики нижней и верхней границ доверительного интервала называются доверительными кривыми надежности
– выборочная дисперсия независимой переменной X. Графики нижней и верхней границ доверительного интервала называются доверительными кривыми надежности 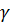 . Уравнение линейной регрессии может быть записано в виде
. Уравнение линейной регрессии может быть записано в виде  . Отсюда следует, что линия регрессии проходит через точку
. Отсюда следует, что линия регрессии проходит через точку  и при
и при 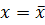 доверительные кривые наиболее близко подходят к линии регрессии.
доверительные кривые наиболее близко подходят к линии регрессии.
Дата добавления: 2018-04-15; просмотров: 701; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
