Лабораторнаяработа № 2. Корреляционный анализ
Цель работы. Овладение методами исследования корреляционной зависимости между несколькими количественными случайными величинами по выборочным данным в MSExcel 2010.
Краткие сведения.Корреляционной зависимостью двух случайных величин Y и X называется функциональная зависимость условного математического ожидания  (или
(или 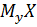 ) одной из них от значения
) одной из них от значения 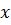 (или
(или  ) другой величины. Корреляционная зависимость может быть представлена в виде уравнения регрессииY по X:
) другой величины. Корреляционная зависимость может быть представлена в виде уравнения регрессииY по X: 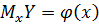 или уравнения регрессииX по Y:
или уравнения регрессииX по Y: 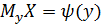 . Если функция
. Если функция  линейная, то корреляционная зависимость называется линейной, если
линейная, то корреляционная зависимость называется линейной, если  нелинейная, то корреляционная зависимость называется нелинейной.
нелинейная, то корреляционная зависимость называется нелинейной.
Основная задача корреляционного анализа – выявление наличия, вида и тесноты корреляционной зависимости между случайными величинами путем точечного и интервального оценивания различных (парных, множественных, частных) коэффициентов корреляции по выборке  …,
…, 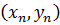 из генеральной совокупности, распределенной по многомерному нормальному закону.
из генеральной совокупности, распределенной по многомерному нормальному закону.
Парная корреляция. Для оценки по выборке наличия и тесноты корреляционной связи между двумя случайными величинами Y и X, имеющими совместное нормальное распределение, используются выборочный коэффициент корреляции и эмпирическое корреляционное отношение.
Выборочный коэффициент корреляции 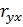 используется для оценки наличия и тесноты парной линейной корреляционной зависимости
используется для оценки наличия и тесноты парной линейной корреляционной зависимости
|
|
|
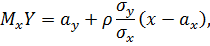
где 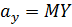 ,
,  генеральный (теоретический) коэффициент корреляции,
генеральный (теоретический) коэффициент корреляции, 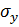 и
и  среднеквадратические отклонения величин Y и Х. Выборочный коэффициент корреляции
среднеквадратические отклонения величин Y и Х. Выборочный коэффициент корреляции 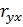 является точечной оценкой генерального коэффициента корреляции
является точечной оценкой генерального коэффициента корреляции  и вычисляется по формуле
и вычисляется по формуле
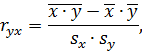
где  и
и 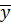 – выборочные общие средние X и Y,
– выборочные общие средние X и Y, 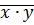 – выборочное общее среднее произведения XY,
– выборочное общее среднее произведения XY,  и
и  – выборочные среднеквадратические отклонения величин X и Y. Выборочный коэффициент корреляции
– выборочные среднеквадратические отклонения величин X и Y. Выборочный коэффициент корреляции 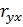 показывает, на сколько величин
показывает, на сколько величин  изменится в среднем зависимая величина Y при увеличении аргумента X на одно
изменится в среднем зависимая величина Y при увеличении аргумента X на одно  и является показателем тесноты парной линейной корреляционной зависимости.
и является показателем тесноты парной линейной корреляционной зависимости.
Свойства выборочного коэффициента корреляции:
· 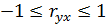 , чем больше
, чем больше 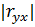 , тем теснее линейная корреляционная зависимость Y и X, т.е. меньше разброс выборочных значений
, тем теснее линейная корреляционная зависимость Y и X, т.е. меньше разброс выборочных значений 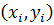 относительно оцененной по выборке линии регрессии
относительно оцененной по выборке линии регрессии
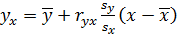 ,
,
которая описывает зависимость условной (групповой) средней 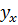 величины Yот значений xвеличиныX;
величины Yот значений xвеличиныX;
· 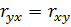 ;
;
· если все выборочные значения умножить на одно и то же число, то величина коэффициента корреляции не изменяется;
· при  корреляционная зависимость представляет линейную функциональную зависимость между Y и X, т.е. все выборочные значения
корреляционная зависимость представляет линейную функциональную зависимость между Y и X, т.е. все выборочные значения 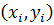 лежат на оцененной линии регрессии
лежат на оцененной линии регрессии 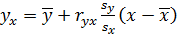 ;
;
|
|
|
· при 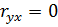 линейная корреляционная зависимость между Y и X отсутствует, их групповые средние
линейная корреляционная зависимость между Y и X отсутствует, их групповые средние 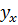 и
и 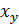 совпадают с их общими средними
совпадают с их общими средними 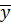 и
и  , а регрессия Y по X принимает вид
, а регрессия Y по X принимает вид 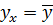 . Равенство
. Равенство 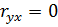 говорит лишь об отсутствии линейной корреляционной зависимости между величинами Y и X, но не об отсутствии корреляции или стохастической зависимости между Y и X.
говорит лишь об отсутствии линейной корреляционной зависимости между величинами Y и X, но не об отсутствии корреляции или стохастической зависимости между Y и X.
Проверка значимости коэффициента корреляции 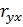 осуществляется путем проверки гипотезы
осуществляется путем проверки гипотезы 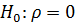 , т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X. При справедливости этой гипотезы статистика
, т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X. При справедливости этой гипотезы статистика

имеет распределение Стьюдента (t-распределение) с числом степеней свободы n-2, где n – объем выборки. Гипотеза 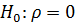 отвергается при уровне значимости
отвергается при уровне значимости 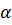 (т.е. выборочный коэффициент корреляции значимо отличается от нуля), если вычисленное по выборке объема
(т.е. выборочный коэффициент корреляции значимо отличается от нуля), если вычисленное по выборке объема  значение
значение  удовлетворяет неравенству
удовлетворяет неравенству
 ,
,
где  – квантиль уровня
– квантиль уровня  распределения Стьюдента с числом степеней свободы
распределения Стьюдента с числом степеней свободы  .
.
Доверительный интервал надежности 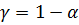 для генерального коэффициента корреляции
для генерального коэффициента корреляции  при значимом выборочном коэффициенте корреляции
при значимом выборочном коэффициенте корреляции  строится с помощью z-преобразования Фишера
строится с помощью z-преобразования Фишера
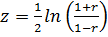 .
.
Распределение статистики  уже при малых объемах выборки близко к нормальному, что позволяет построить доверительный интервал для ее математического ожидания и от него перейти к доверительному интервалу для генерального коэффициента корреляции
уже при малых объемах выборки близко к нормальному, что позволяет построить доверительный интервал для ее математического ожидания и от него перейти к доверительному интервалу для генерального коэффициента корреляции  , который имеет вид
, который имеет вид
|
|
|
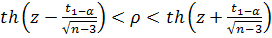 ,
,
где  – гиперболический тангенс
– гиперболический тангенс 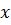 , а
, а 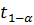 определяется по функции Лапласа из условия
определяется по функции Лапласа из условия 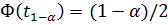 .
.
Для определения наличия и тесноты любой (линейной или нелинейной) корреляционной связи используется эмпирическое корреляционноеотношениеY к X
 ,
,
которое тем больше, чем большее влияние на вариацию Y оказывает изменчивость X по сравнению с неучтенными факторами. Здесь 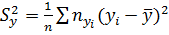 – общая выборочная дисперсия величины Y,
– общая выборочная дисперсия величины Y, 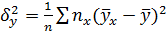 – межгрупповая дисперсия Y. Свойства эмпирического корреляционного отношения:
– межгрупповая дисперсия Y. Свойства эмпирического корреляционного отношения:
· 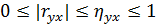 ;
;
· 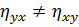 ;
;
· при 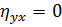 корреляционная связь между Y и Xотсутствует;
корреляционная связь между Y и Xотсутствует;
· при 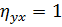 между Y и X существует функциональная зависимость;
между Y и X существует функциональная зависимость;
· при 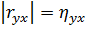 между Y и X существует линейная корреляционная зависимость.
между Y и X существует линейная корреляционная зависимость.
Величина  называется эмпирическим коэффициентом детерминации, она показывает, какая часть общей вариации Y обусловлена вариацией X.
называется эмпирическим коэффициентом детерминации, она показывает, какая часть общей вариации Y обусловлена вариацией X.
Многомерный корреляционный анализ исследует корреляционную зависимость совокупности случайных величин  имеющих совместное нормальное распределение. Корреляционная матрица
имеющих совместное нормальное распределение. Корреляционная матрица 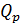 , составленная из парных генеральных коэффициентов корреляции
, составленная из парных генеральных коэффициентов корреляции  величин
величин 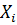 и
и 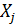 ,
,
|
|
|
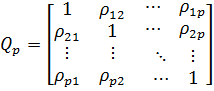 ,
,
характеризует линейную корреляционную зависимость между парами величин 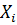 и
и 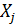 этой совокупности. Основная задача многомерного корреляционного анализа состоит в оценке корреляционной матрицы
этой совокупности. Основная задача многомерного корреляционного анализа состоит в оценке корреляционной матрицы 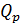 по выборочным данным. Такой оценкой является матрица выборочных коэффициентов корреляции
по выборочным данным. Такой оценкой является матрица выборочных коэффициентов корреляции
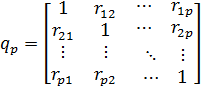 ,
,
в которой 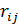 – выборочные коэффициенты корреляции между величинами
– выборочные коэффициенты корреляции между величинами 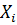 и
и 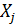 . Матрицы
. Матрицы 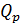 и
и  симметричные, поэтому при вычислении матрицы
симметричные, поэтому при вычислении матрицы  приводятся только элементы, расположенные на главной диагонали и под ней.
приводятся только элементы, расположенные на главной диагонали и под ней.
Теснота линейной корреляционной связи одной из величин 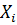 с совокупностью остальных
с совокупностью остальных 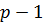 величин
величин 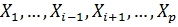 оценивается выборочным коэффициентом множественной корреляции
оценивается выборочным коэффициентом множественной корреляции
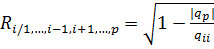 ,
,
где 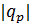 – определитель матрицы
– определитель матрицы  ,
, 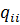 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента  матрицы
матрицы  . В частности, для трех величин
. В частности, для трех величин  выборочный коэффициент множественной корреляции
выборочный коэффициент множественной корреляции 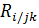 вычисляется по формуле
вычисляется по формуле
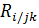 =
= 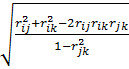 .
.
Выборочный коэффициент множественной корреляции принимает значения от 0 до 1. Чем ближе значение 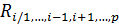 к единице тем теснее линейная корреляционная связь
к единице тем теснее линейная корреляционная связь 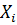 с остальными величинами
с остальными величинами 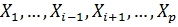 . Величина
. Величина 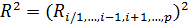 называется выборочным множественным коэффициентом детерминации, которая показывает долю вариации переменной
называется выборочным множественным коэффициентом детерминации, которая показывает долю вариации переменной 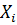 объясняемую вариацией остальных переменных. Множественный коэффициент корреляции
объясняемую вариацией остальных переменных. Множественный коэффициент корреляции 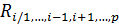 значим при уровне значимости
значим при уровне значимости 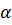 , если вычисленное значение F-статистики
, если вычисленное значение F-статистики
 ,
,
где 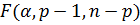 значение
значение  -критерия на уровне значимости
-критерия на уровне значимости 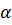 при числе степеней свободы
при числе степеней свободы 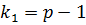 и
и 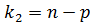 .
.
Частные коэффициенты корреляции. Если величины из совокупности  коррелируют друг с другом, то на величинах парных коэффициентов корреляции
коррелируют друг с другом, то на величинах парных коэффициентов корреляции 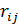 переменных
переменных 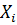 и
и 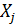 сказывается влияние и других переменных совокупности, что приводит к искажению значений коэффициентов корреляции
сказывается влияние и других переменных совокупности, что приводит к искажению значений коэффициентов корреляции 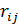 . Для оценки линейной корреляционной зависимости между величинами
. Для оценки линейной корреляционной зависимости между величинами 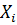 и
и 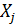 , очищенной от влияния других величин совокупности, используется выборочный частный коэффициент корреляции
, очищенной от влияния других величин совокупности, используется выборочный частный коэффициент корреляции 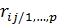 .Он определяется соотношением
.Он определяется соотношением
 ,
,
где 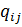 ,
, 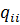 ,
,  алгебраические дополнения соответственно элементов
алгебраические дополнения соответственно элементов 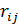 ,
,  ,
,  матрицы выборочных коэффициентов корреляции
матрицы выборочных коэффициентов корреляции  . Например, для совокупности из трех случайных величин
. Например, для совокупности из трех случайных величин  выборочные частные коэффициенты корреляции
выборочные частные коэффициенты корреляции 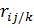 находятся по формуле
находятся по формуле
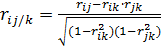 .
.
Частный коэффициент корреляции принимает значения от -1 до +1. Значимость частного коэффициента корреляции при заданном уровне α определяется также, как и значимость коэффициента корреляции с помощью t-статистики: если
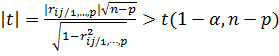 ,
,
то частный коэффициент корреляции 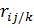 значимо отличается от нуля. Матрица частных коэффициентов корреляции является также симметричной, элементы ее главной диагонали равны единице.
значимо отличается от нуля. Матрица частных коэффициентов корреляции является также симметричной, элементы ее главной диагонали равны единице.
Дата добавления: 2018-04-15; просмотров: 587; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
