Лабораторная работа № 5. Нелинейная парная регрессия
Цель работы. Освоение способов перехода от нелинейной взаимосвязи зависимой и объясняющей переменной к линейной модели; освоение построения по выборочным данным нелинейной модели парной регрессии; оценка значимости построенной модели и ее прогностических свойств; оценка точности и надежности параметров модели; построение прогнозов значений зависимой переменной в MSExcel 2010. Интерпретация модели.
Краткие сведения. В парной линейной регрессии взаимосвязь наблюдаемых в выборке значений  зависимой переменной
зависимой переменной  и значений
и значений 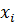 фактора Xописывается линейной по
фактора Xописывается линейной по 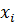 и линейной по параметрам зависимостью
и линейной по параметрам зависимостью  . Она не всегда наилучшим образом отражает существующую взаимосвязь
. Она не всегда наилучшим образом отражает существующую взаимосвязь  и X. Поэтому наряду с парной линейной регрессией рассматривают и нелинейные модели парной регрессии, в которых исследуются нелинейные взаимосвязи
и X. Поэтому наряду с парной линейной регрессией рассматривают и нелинейные модели парной регрессии, в которых исследуются нелинейные взаимосвязи  и
и 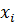 .
.
Различают два класса нелинейных моделей регрессии:
· регрессии,нелинейные относительно объясняющих переменных, но линейные относительно параметров модели, например,  ,
,  или
или 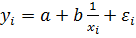 ;
;
· регрессии нелинейные по параметрам, например,  или
или  .
.
1.Нелинейные по объясняющим переменным, но линейные по параметрам, уравнения регрессии введением новых объясняющих переменных сводятся к линейным регрессионным уравнениям и оцениваются методом наименьших квадратов. Например: нелинейная модель  введением новой переменной
введением новой переменной  приводится к линейной модели парной регрессии
приводится к линейной модели парной регрессии  ;нелинейная модель
;нелинейная модель 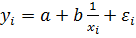 введением новой объясняющей переменной
введением новой объясняющей переменной  также приводится к линейной модели парной регрессии
также приводится к линейной модели парной регрессии  ; нелинейная модель
; нелинейная модель  введением новой объясняющей переменной
введением новой объясняющей переменной  приводится к линейной модели множественной регрессии
приводится к линейной модели множественной регрессии  . Параметры нелинейных по объясняющим переменным, но линейных по параметрам, уравнений регрессии совпадают с параметрами преобразованного линейного уравнения регрессии. Ошибки регрессии
. Параметры нелинейных по объясняющим переменным, но линейных по параметрам, уравнений регрессии совпадают с параметрами преобразованного линейного уравнения регрессии. Ошибки регрессии  преобразованной линейной модели должны удовлетворять предпосылкам линейной регрессии. Оценки метода наименьших квадратов параметров преобразованной линейной модели являются оценками параметров исходной нелинейной модели. Например, для нелинейной модели
преобразованной линейной модели должны удовлетворять предпосылкам линейной регрессии. Оценки метода наименьших квадратов параметров преобразованной линейной модели являются оценками параметров исходной нелинейной модели. Например, для нелинейной модели 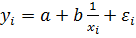 оцененным уравнением регрессиибудет
оцененным уравнением регрессиибудет  , где
, где  и
и  оценки метода наименьших квадратов линейной модели
оценки метода наименьших квадратов линейной модели  с
с  .
.
|
|
|
2.Регрессии нелинейные по параметрам разделяются на внутренне линейные и внутренне нелинейные модели. Внутренне линейные модели с помощью соответствующих преобразований приводятся к линейному виду и затем оцениваются методом наименьших квадратов. При этом нужно помнить, что свойства оценок параметров и модели (получаемые, например, с помощью функции «Регрессия» в MSExcel) относятся к преобразованной линейной модели, а не к исходной нелинейной модели.Внутренне нелинейные модели не могут быть приведены к линейному виду. Внутренне нелинейные модели оцениваются специальными методами. В работе рассматриваются только внутренне линейные модели.
|
|
|
Рассмотрим наиболее широко применяемые при моделировании социально-экономических процессов внутренне линейные модели регрессии и их преобразования к линейному виду.
Мультипликативная модель (степенная с постоянной эластичностью  )
)
 ,
,
 – мультипликативная случайная ошибка регрессии. Эта модель нелинейная относительно оцениваемых параметров aиb. Прологарифмировав это уравнение, получим
– мультипликативная случайная ошибка регрессии. Эта модель нелинейная относительно оцениваемых параметров aиb. Прологарифмировав это уравнение, получим
 .
.
Введя новые величины  ,
,  ,
,  и
и  , получим линейное уравнение
, получим линейное уравнение
 ,
,
в котором ошибки регрессии  должны удовлетворять предпосылкам линейной регрессии. Получив МНК оценки
должны удовлетворять предпосылкам линейной регрессии. Получив МНК оценки 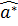 и
и  параметров линеаризованной модели, одновременно получаем оценку параметра bнелинейной модели, а оценка параметра a находится как
параметров линеаризованной модели, одновременно получаем оценку параметра bнелинейной модели, а оценка параметра a находится как  .
.
Экспоненциальная модель (с постоянным темпом прироста b)
 (или
(или  ).
).
Прологарифмировав получим  . Введя новые величины
. Введя новые величины  и
и  , получим линейное уравнение
, получим линейное уравнение
|
|
|
 ,
,
в котором ошибки регрессии  должны удовлетворять предпосылкам линейной регрессии. МНК оценки
должны удовлетворять предпосылкам линейной регрессии. МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
Экспоненциальная модель
 (или
(или  ).
).
Прологарифмировав получим  . Введя новую зависимую переменную
. Введя новую зависимую переменную  и новую объясняющую переменную
и новую объясняющую переменную  , получим линейное уравнение
, получим линейное уравнение
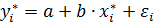 .
.
МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
параметров линеаризованной модели являются оценками параметров исходной нелинейной модели.
Показательная модель (с постоянным темпом прироста равнымlnb)

логарифмированием приводится к виду  и введением новых величин
и введением новых величин  ,
,  и
и  преобразуется в линейную модель
преобразуется в линейную модель 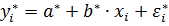 . Ошибки регрессии
. Ошибки регрессии  должны удовлетворять предпосылкам линейной регрессии. По МНК оценкам
должны удовлетворять предпосылкам линейной регрессии. По МНК оценкам 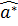 и
и  параметров линеаризованной модели оценки параметров aи b показательной модели находятся как
параметров линеаризованной модели оценки параметров aи b показательной модели находятся как  и
и  .
.
Обратная модель

приводится к линеаризованному виду  с помощью замены
с помощью замены  . Более сложная обратная модель (логистическая)
. Более сложная обратная модель (логистическая)
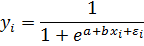
приводится к линеаризованному виду  с помощью замены
с помощью замены  . В обеих случаях МНК оценки
. В обеих случаях МНК оценки  и
и  параметров линеаризованной модели являются оценками параметров обратной модели.
параметров линеаризованной модели являются оценками параметров обратной модели.
Примеры внутренне нелинейных моделей (не приводимых к линейным по параметрам зависимостям):  ,
,  ,
, 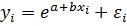 ,
,  ,
,  ,
,  .
.
|
|
|
Линеаризация многофакторных нелинейных регрессионных моделей производится с использованием тех же приемов. Например, производственная функция Кобба-Дугласа 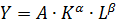 логарифмированием приводится к виду
логарифмированием приводится к виду  и заменами
и заменами 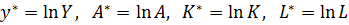 преобразуется к линейному по параметрам уравнение
преобразуется к линейному по параметрам уравнение  .
.
Для сопоставления различных линейных и нелинейных регрессионных моделей по их прогностическому качеству используются индекс корреляции (корреляционное отношение)

и средняя ошибка аппроксимации
 .
.
Здесь  – рассчитанные по уравнению регрессии значения зависимой переменной,
– рассчитанные по уравнению регрессии значения зависимой переменной,  – выборочная средняя значений зависимой переменной, n – объем выборки. Индекс корреляции характеризует разброс выборочных значений относительно линии регрессии
– выборочная средняя значений зависимой переменной, n – объем выборки. Индекс корреляции характеризует разброс выборочных значений относительно линии регрессии  .
.  .Чем больше значение
.Чем больше значение  , тем меньше разброс выборочных значений вокруг линии регрессии (тем лучше качество подгонки уравнения регрессии к выборочным данным). Если
, тем меньше разброс выборочных значений вокруг линии регрессии (тем лучше качество подгонки уравнения регрессии к выборочным данным). Если  равно или близко к нулю, то оцененная модель непригодна, она не объясняет изменение зависимой переменной изменением объясняющей переменной, т. е. построенная модель не лучше модели
равно или близко к нулю, то оцененная модель непригодна, она не объясняет изменение зависимой переменной изменением объясняющей переменной, т. е. построенная модель не лучше модели  . Квадрат индекса корреляции называется коэффициентом детерминациии обозначается
. Квадрат индекса корреляции называется коэффициентом детерминациии обозначается  , т.е.
, т.е.  . Он показывает долю вариации зависимой переменной Y объясняемую вариацией фактора X в построенной модели регрессии. Средняя ошибка аппроксимации A характеризует среднее относительное отклонение выборочных значений от построенной линии регрессии
. Он показывает долю вариации зависимой переменной Y объясняемую вариацией фактора X в построенной модели регрессии. Средняя ошибка аппроксимации A характеризует среднее относительное отклонение выборочных значений от построенной линии регрессии  .
.
Проверка статистической значимости уравнения нелинейного регрессии (гипотезы  ) проводится по F-критерию Фишера
) проводится по F-критерию Фишера  , который имеет F-распределение Фишера-Снедекора с
, который имеет F-распределение Фишера-Снедекора с 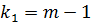 и
и  степенями свободы, где
степенями свободы, где 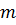 – число коэффициентов в уравнении регрессии, а n– объем выборки. Оцененное уравнение нелинейной регрессии статистически незначимо, если вычисленное значение F-критерия меньше критического
– число коэффициентов в уравнении регрессии, а n– объем выборки. Оцененное уравнение нелинейной регрессии статистически незначимо, если вычисленное значение F-критерия меньше критического  . Если
. Если  , то оцененное уравнение нелинейной регрессии статистически значимо, т.е. влияние фактора
, то оцененное уравнение нелинейной регрессии статистически значимо, т.е. влияние фактора 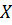 на исследуемый признак
на исследуемый признак  может быть описано оцененным уравнением нелинейной регрессии.
может быть описано оцененным уравнением нелинейной регрессии.  – квантиль уровня
– квантиль уровня 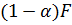 -распределения Фишера-Снедекора с
-распределения Фишера-Снедекора с 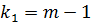 и
и  степенями свободы.
степенями свободы.
Дата добавления: 2018-04-15; просмотров: 987; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
