Вектор как направленный отрезок
Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
 Здесь точка А – начало вектора, а точка В – его конец. У вектора есть два параметра: его длина и направление.
Здесь точка А – начало вектора, а точка В – его конец. У вектора есть два параметра: его длина и направление.
Длина вектора – это длина отрезка, соединяющего начало и конец вектора. Длина вектора 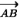 обозначается
обозначается 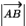
Равенство векторов.
Два вектора называются равными, если они сонаправленные и имеют равные модули.
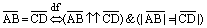 , т.е, если они совмещаются параллельным переносом (существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно).
, т.е, если они совмещаются параллельным переносом (существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно).
Операция умножения вектора на число и её свойства.
Произведением вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа, а направление совпадает с направлением умножаемого вектора, если число больше нуля, и противоположно ему, если число меньше нуля. (Если совсем просто, то это вектор в n раз длиннее данного, где n - данное число). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор
Свойства операций умножения вектора на число:
1) Сочетательное свойство умножения 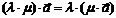
2) Первое распределительное свойство 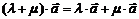
3) Второе распределительное свойство 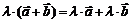 .
.
4) Нейтральным числом по умножению является единица, то есть 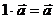 .
.
При умножении вектора на единицу с ним не производится никаких геометрических преобразований.
|
|
|
5) 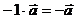
6) 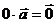
Здесь 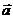 и
и 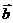 - произвольные векторы, а
- произвольные векторы, а  и
и 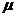 - произвольные числа.
- произвольные числа.
Коллинеарные векторы.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Выражение коллинеарных векторов друг через друга.
Пусть 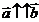 ,и пусть модуль вектора
,и пусть модуль вектора 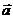 в
в 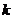 раз превышает модуль вектора
раз превышает модуль вектора 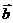 , т. е.
, т. е. 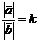 .
.
Тогда 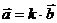 .Таким образом, в векторе
.Таким образом, в векторе 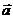 укладывается
укладывается 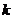 векторов
векторов 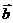 .
.
Пусть теперь 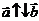 и
и 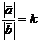 . Тогда
. Тогда 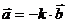 .
.
Сумма векторов и её свойства.
Суммой векторов 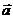 с координатами a1, a2 и
с координатами a1, a2 и 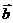 с координатами b1, b2 называется такой третий вектор
с координатами b1, b2 называется такой третий вектор 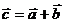 с координатами а1 + b1, a2 + b2. Начало этого вектора совпадает с началом вектора
с координатами а1 + b1, a2 + b2. Начало этого вектора совпадает с началом вектора 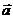 , а конец – с концом вектора
, а конец – с концом вектора 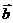 при условии, что начало вектора
при условии, что начало вектора 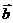 совпадает с концом вектора
совпадает с концом вектора 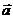 (правило треугольников)
(правило треугольников) 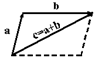
А при совмещенных началах этих трех векторов, векторы 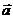 и
и 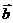 служат сторонами параллелограмма, а вектор c -- его диагональю .
служат сторонами параллелограмма, а вектор c -- его диагональю . 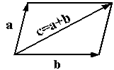 (правило параллелограмма)
(правило параллелограмма)
Свойства суммы векторов:
1° 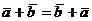 - коммутативность
- коммутативность
2° 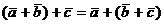 - ассоциативность
- ассоциативность
3° 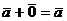
4° 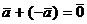
Противоположный вектор.
Два вектора называются противоположными, если они противоположно направлены и их длины равны.
Разность векторов.
|
|
|
Разностью векторов  и
и  с координатами
с координатами 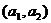 и
и 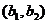 называется вектор
называется вектор 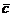 с координатами
с координатами 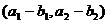 , т.е. это такой вектор , который в сумме с вектором даст вектор.
, т.е. это такой вектор , который в сумме с вектором даст вектор.
2. Экстремумы: определение, необходимое условие, достаточные условия.
Экстре́мумы — максимальные или минимальные значения функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума
Точка 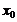 называется точкой локального максимума функции
называется точкой локального максимума функции 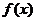 , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех 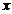 из этой окрестности выполняется неравенство:
из этой окрестности выполняется неравенство: 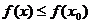 .
.
Точка 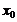 называется точкой локального минимума функции
называется точкой локального минимума функции 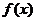 , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех 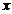 из этой окрестности
из этой окрестности 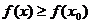 .
.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка 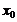 называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции 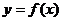 , если для всех
, если для всех 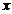 из окрестности этой точки будет справедливо строгое неравенство
из окрестности этой точки будет справедливо строгое неравенство 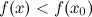 .
.
|
|
|
Точка 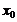 называется точкой строгого локального минимума функции
называется точкой строгого локального минимума функции 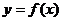 , если для всех
, если для всех 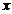 из окрестности этой точки будет справедливо строгое неравенство
из окрестности этой точки будет справедливо строгое неравенство 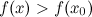 .
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
необходимое условие
Если функция 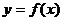 имеет экстремум в точке
имеет экстремум в точке 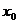 , то ее производная либо равна нулю
, то ее производная либо равна нулю 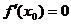 , либо не существует.
, либо не существует.
Точки, в которых производная равна нулю: 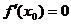 , называются стационарными точками функции.
, называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения 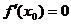 ), либо это точки, в которых производная
), либо это точки, в которых производная 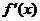 не существует. Не в каждой своей критической точке функция обязательно имеет максимум или минимум
не существует. Не в каждой своей критической точке функция обязательно имеет максимум или минимум
Достаточные условия
(Первое достаточное условие экстремума)
Пусть для функции 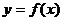 выполнены следующие условия:
выполнены следующие условия:
1. функция непрерывна в окрестности точки 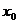 ;
;
2. 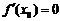 или
или 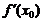 не существует;
не существует;
3. производная 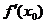 при переходе через точку
при переходе через точку 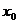 меняет свой знак.
меняет свой знак.
Тогда в точке 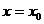 функция
функция 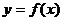 имеет экстремум,
имеет экстремум,
|
|
|
причем это минимум, если при переходе через точку 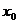 производная меняет свой знак с минуса на плюс;
производная меняет свой знак с минуса на плюс;
максимум, если при переходе через точку 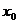 производная меняет свой знак с плюса на минус.
производная меняет свой знак с плюса на минус.
Если производная 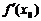 при переходе через точку
при переходе через точку 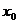 не меняет знак, то экстремума в точке
не меняет знак, то экстремума в точке 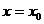 нет.
нет.
Таким образом, для того чтобы исследовать функцию 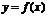 на экстремум, необходимо:
на экстремум, необходимо:
1. найти производную 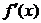 ;
;
2. найти критические точки, то есть такие значения  , в которых
, в которых 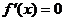 или
или 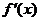 не существует;
не существует;
3. исследовать знак производной слева и справа от каждой критической точки;
4. найти значение функции в экстремальных точках.
(Второе достаточное условие экстремума)
Пусть для функции 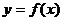 выполнены следующие условия:
выполнены следующие условия:
1. она непрерывна в окрестности точки 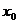 ;
;
2. первая производная 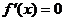 в точке
в точке 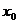 ;
;
3. 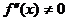 в точке
в точке 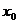 .
.
Тогда в точке 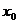 достигается экстремум, причем, если
достигается экстремум, причем, если 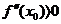 , то в точке
, то в точке 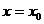 функция
функция 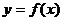 имеет минимум; если
имеет минимум; если 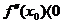 , то в точке
, то в точке 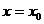 функция
функция 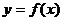 достигает максимум.
достигает максимум.
Билет 4
1. Линейная комбинация векторов.
Линейной комбинацией векторов 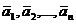 называется вектор
называется вектор 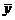 , получаемый из векторов этой системы путем умножения их на коэффициенты линейной комбинации
, получаемый из векторов этой системы путем умножения их на коэффициенты линейной комбинации 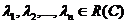 и сложения, т. е.
и сложения, т. е. 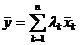
Разложение вектора на плоскости по двум неколлинеарным векторам.
Любой вектор можно разложить, и при том единственным образом, по двум данным неколлинеарным векторам. Т. е. если 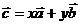 , где
, где 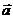 и
и 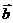 – данные векторы, x и y – некоторые числа, то говорят, что вектор
– данные векторы, x и y – некоторые числа, то говорят, что вектор 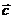 разложен на векторы
разложен на векторы 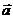 и
и 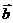 , причем x и y – коэффициенты разложения, определяемые единственным образом.
, причем x и y – коэффициенты разложения, определяемые единственным образом.
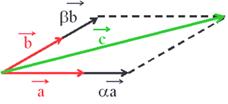
Компланарные векторы.
Компланарные векторы — это векторы, лежащие в одной плоскости или в параллельных плоскостях
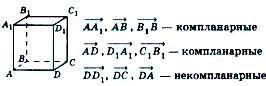
|
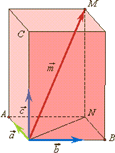
Разложение вектора по трем некомпланарным векторам.
Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом. Вектор 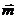 разложен по трём некомпланарным векторам
разложен по трём некомпланарным векторам 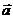 ,
, 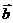 и
и 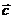 , если его можно представить в виде
, если его можно представить в виде 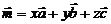 , где
, где  ,
,  и
и 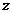 — коэффициенты разложения. Числа x, y, z называются координатами вектора
— коэффициенты разложения. Числа x, y, z называются координатами вектора 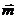 в данном базисе. В этом случае пишут
в данном базисе. В этом случае пишут 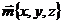
Дата добавления: 2018-04-05; просмотров: 989; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
