Вывести условия параллельности, совпадения и перпендикулярности прямых на плоскости

Условие параллельности двух прямых (вывод):

а) Если прямые 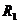и заданы уравнениями с угловым коэффициентом и параллельны, то 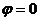. Тогда 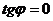и из формулы

или . Таким образом, достаточное условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е..

Условия перпендикулярности двух прямых (вывод):

а) Если прямые 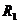и заданы уравнениями с угловым коэффициентом и перпендикулярны, то . Так как , то и 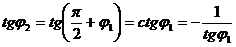, т.е. .

Таким образом, , необходимое и достаточное условие их перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.

б) Если уравнения прямых заданы в общем виде A₁x + B₁y + C₁ = 0,

A₂x + B₂y + C₂ = 0,

, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A₁A₂ + B₁B₂ = 0.

Условие совпадение двух прямых

На плоскости заданы прямые 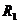, общими уравнениями: _{; . (1)}

Очевидно, совпадение двух прямых есть частный случай параллельности. Поэтому должно быть О _(2).Обозначая общую величину обоих отношений через , имеем _{, (3),}

Откуда _{, .} Тогда уравнение системы (1) имеет вид _,или _.Если уравнения (1) изображают одну и ту же прямую, то одни и те же координаты х, y удовлетворяют как уравнению (4), так и второму уравнению системы (1). Поэтому, если вычтем из уравнения (4) второе уравнение (1), то получим или 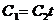_.Сопоставляя это с (3), находим _.Это и есть условие совпадения двух прямых, которое говорит о том, что коэффициенты совпадающих прямых пропорциональны, то есть одно уравнение получается из второго путем умножения на некоторое постоянное число (число )

2. Производная: физические задачи, приводящие к понятию производной, определение.

физические задачи, приводящие к понятию производной

Задача о скорости движущейся точки.

Пусть s = s (t) представляет закон прямолинейного движения материальной точки.

Это уравнение выражает путь s, пройденный точкой, как функцию времени t.

Обозначим через Δs путь, пройденный за промежуток времени Δt от момента t до t + Δt , т. е.
Δs = s(t + Δt ) - s (t). Отношение называется средней скоростью точки за время от t до t + Δt.

Чем меньше Δt, т. е. чем короче промежуток времени от t до t + Δt, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости v в данный момент t, определив ее как предел средней скорости за промежуток от t до t + Δt, когда :

Величина v называется мгновенной скоростью точки в данный момент t.

Задача о касательной к данной кривой.

Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести касательную к данной кривой в данной точке .

Так как точка касания 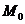д ана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. — тангенс угла наклона касательной к положительному направлению оси Ох (рис.).
Через точки и проведем секущую

Из рис. видно, что угловой коэффициент секущей равен отношению , где .

Угловой коэффициент касательной к данной кривой в точке 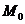можно найти на основании следующего определения: касательной к кривой в точке 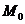называется прямая , угловой коэффициент которой равен пределу углового коэффициента секущей , когда 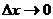. Отсюда следует, что
Производной функции f(x) в точке х=х₀ называется отношение приращения функции 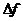в этой точке к приращению аргумента, при стремлении последнего к нулю.

_при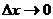

Дата добавления: 2018-04-05; просмотров: 2715; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!