Геометрическая интерпретация (уравнения касательной и нормали)
Рассмотрим график функции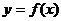 
.
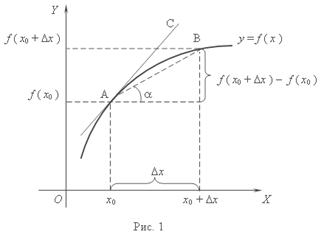
Из рис.1 видно, что для любых двух точек A и B графика функции: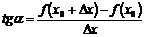 
где 
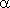- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то 
x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
1. Касательной к графику функции в точке (х0; f(х0)) называется предельное положение секущей (АС).
Уравнение касательной: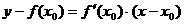 
2. Прямая, перпендикулярная касательной (АС) в точке (х0; f(х0), называется нормалью к графику функции.
Уравнение нормали: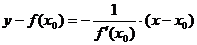 
Билет 11
1. Вывести формулу для вычисления расстояния от точки до прямой на плоскости.
Если задана точка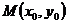 
, то расстояние до прямой 
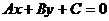определяется как 
.
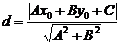Доказательство. Пусть точка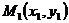 
– основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками 
и 
: 
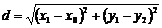(1)
Координаты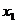 
и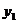 
могут быть найдены как решение системы уравнений: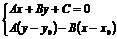 
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку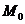 
перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: 
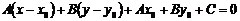, то, решая, получим:
,
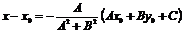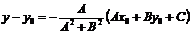
Подставляя эти выражения в уравнение (1), находим:
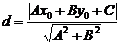. Теорема доказана.
2. Доказательство первого замечательного предела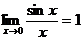 
.
Доказательство
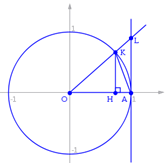
Рассмотрим односторонние пределы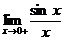 
и 
и докажем, что они равны 1.
Пусть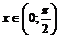 
. Отложим этот угол на единичной окружности 
.
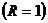Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке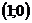 
. Точка H — проекция точки K на ось OX.
Очевидно, что:
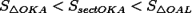(1)
(где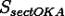 
— площадь сектора 
)
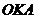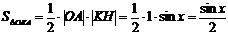
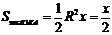
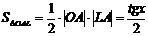
(из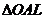 
: 
)
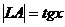Подставляя в (1), получим:
< 
< 
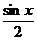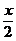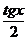
Так как при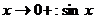 
>0, x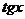>0, 
>0:
< 
< 
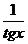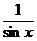
Умножаем на 
:
< 
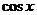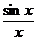< 1
Перейдём к пределу:
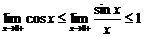
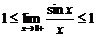
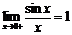
Найдём левый односторонний предел:
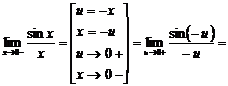
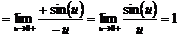
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Билет 12
1. Вывести общее уравнение плоскости.
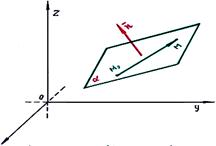Для получения общего уравнения плоскости мы воспользуемся теоремой, согласно которой, плоскость 
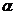можно определить, задавая произвольную точку 
,
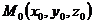принадлежащую этой плоскости, и направление перпендикуляра, нормали, к этой плоскости – вектор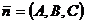 
:
Пусть точка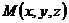 
принадлежит плоскости 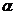. Тогда вектор 
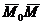также принадлежит плоскости 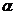(в рассматриваемом случае вектор 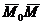приложен к точке 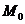). Так как вектор 
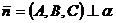, то векторы 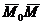и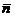 
взаимно перпендикулярны. Используя свойство скалярного произведения для векторов 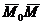и 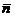, можем записать: × = 
× 
=
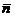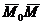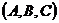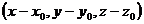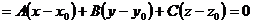, (1)
уравнение (1) приводится к виду: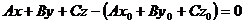 
, сохраняя свойство принадлежности: 
.
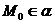Имея выражение (1), можем предположить, что выражение, содержащее переменные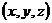 
в первой степени (то есть линейное выражение): 
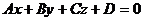, (2)
является уравнением некоторой плоскости пространства. Действительно, пусть некоторая точка 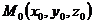принадлежит геометрической фигуре, определяемой выражением (2). Это значит, что имеем тождество: 
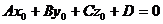. (3)
Вычитая из равенства (2) равенство (3), получаем выражение (1), которое определяет плоскость, определяемую точкой 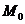и вектором нормали 
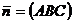. Уравнение (2) за его свойство представлять любую плоскость пространства называют общим уравнением плоскости.
Дата добавления: 2018-04-05; просмотров: 578; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!