Получить уравнение плоскости в отрезках и уравнение плоскости, проходящей через три заданные точки (с выводом)
Уравнение плоскости в отрезках имеет вид: 
, где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.
Пусть в трехмерном пространстве задана прямоугольная система координат Oxyz.
В прямоугольной системе координат Oxyz в трехмерном пространстве уравнение вида , где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках. Такое название не случайно. Абсолютные величины чисел a, b и c равны длинам отрезков, которые плоскость отсекает на координатных осях Ox, Oy и Oz соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) откладываются отрезки на координатных осях. Действительно, координаты точек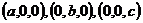 
удовлетворяют уравнению плоскости в отрезках:
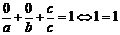
Рисунок, поясняющий этот момент.
Уравнение плоскости, проходящей через три заданные точки (с выводом).
Пусть даны три точки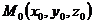 
, 
, 
, которые лежат в одной плоскости. Пусть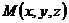 
произвольная точка этой плоскости. Тогда векторы 
, 
, 
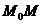лежат в одной плоскости и их смешанное произведение равно нулю: 
Расписывая смешанные произведения в координатной форме, получим:
Раскроем определитель по первой строке:
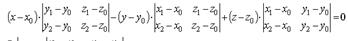
Если ввести обозначения:
,
то получим 
, уравнение плоскости
2. Предел функции: определение свойства.
Число А называется пределом функции f(x) при 
, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается 
.
|
|
|
Свойства пределов функции
1. Предел суммы/разности двух функций равен сумме/разности их пределов:
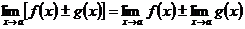
2. Предел произведения двух функций равен произведению их пределов:
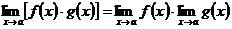
3. Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю: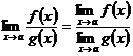 
, 
4. Константу можно выносить за знак предела: 
5. Предел степени с натуральным показателем равен степени предела:
, 
Непрерывность: определение, односторонние пределы и виды разрывов (с примерами).
Непрерывность: определение
Говорят, что функция действительного переменного 
является непрерывной в точке 
( 
- множество действительных чисел), если для любой последовательности 
, такой, что
, выполняется соотношение 
.
Односторонний предел— предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Число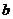 
называется правым пределом функции в точке 
, если для 
найдется 
такое, что для любого 
и < 
< 
, выполняется неравенство (рис. 1). Правый предел обозначается 
|
|
|
Число 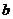называется левым пределом функции в точке , если для найдется такое, что для любого и 
< < , выполняется неравенство 
(рис. 2). Левый предел обозначается 
Виды разрывов
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.
Дата добавления: 2018-04-05; просмотров: 518; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!