Физический смысл векторного произведения
-момент силы 
относительно тоски О; 
-радиус-вектор точки приложения силы , тогда 
причем если перенести в точку О, то тройка , 
, должна быть ориентирована как вектор базиса.
Свойства векторного произведения.
1. антикоммутативность 
;
2. свойство дистрибутивности 
или 
;
3. сочетательное свойство 
или 
, где 
- произвольное действительное число.
Вычисление векторного произведения «в координатах» (с выводом).
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты 
, 
, 
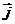, во второй строке находятся координаты вектора 
, а в третьей – координаты вектора 
в заданной прямоугольной системе координат:
Если разложить этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
2. Нахождение производной функции, заданной параметрически (с обоснованием).
Вывод формулы производной параметрически заданной функции.
Пусть 
, 
определены и дифференцируемы при 
, причем 
и 
имеет обратную функцию 
.
Сначала переходим от параметрического задания к явному. При этом получаем сложную функцию 
, аргументом которой является x. По правилу нахождения производной сложной функции имеем: 
. Так как и обратные функции, то по формуле производной обратной функции 
, поэтому 
Нахождение производной функции, заданной неявно (на примере).
|
|
|
Если независимая переменная 
и функция 
связаны уравнением вида 
, которое не разрешено относительно , то функция называется неявной функцией переменной .
Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументу x, считая y – функцией от x, и после этого выразить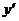 
.
Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции.
Пример.
Найти производную неявной функции 
.
Решение.
Производная неявно заданной функции всегда представляется в виде выражения, содержащего x и y: 
. Чтобы прийти к такому результату, продифференцируем обе части равенства:
Разрешим полученное уравнение относительно производной:
Билет 8
1. Смешанное произведение векторов.
Сме́шанное произведе́ние 
векторов —скалярное произведение вектора 
на векторное произведение векторов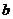 
и 
: 
.
Его геометрический смысл.
Если тройка векторов 
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 
. В случае левой тройки смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: 
. Если 
, 
и 
компланарны, то их смешанное произведение равно нулю.
|
|
|
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах , и равен модулю смешанного произведения этих векторов: 
Объем пирамиды, построенной на этой тройке векторов равен: 
Вычисление смешанного произведения через координаты векторов (вывод).
Пусть заданы вектора: а = ахi + аyj + аzk , b = bхi + byj + bzk и с = схi + сyj + сzk
Найдем их смешанное произведение, используя выражение в координатах для векторного и скалярного произведений:
.
Итак, 
.
Следовательно, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
2. Производная сложной функции, производная обратной функции (с доказательствами).
Дата добавления: 2018-04-05; просмотров: 410; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!