Вывести уравнение прямой на плоскости с угловым коэффициентом и уравнение прямой в отрезках на осях
Уравнение прямой с угловым коэффициентом имеет вид  , где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
, где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy (для прямой параллельно оси ординат угловой коэффициент не определен).
Пусть прямая l не параллельна оси Оу (рис.1). Обозначим точку пересечения прямой l с осью Оу буквой В(О;в), а угол между положительным направлением оси Ох и прямой l обозначим угол, отсчитываемый от оси Ох против часовой стрелки () 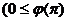 , называется углом наклона прямой l к оси Ох.
, называется углом наклона прямой l к оси Ох.

Выведем уравнение прямой l.
Пусть М(х,у) – произвольная точка прямой l с текущими координатами х,у. Из прямоугольного треугольника ВМN (рис.1) имеем:  (1)
(1)
Отсюда  , или
, или  и окончательно
и окончательно 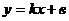 где
где  - Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
- Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
Уравнение 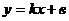 называется уравнением прямой с угловым коэффициентом.
называется уравнением прямой с угловым коэффициентом.
Число в – это величина отрезка, отсекаемого прямой на оси ординат.
Уравнение прямой в отрезках на осях вывод
Если известны точки пересечения прямой с осями координатами  и
и  . Для этого воспользуемся уравнением прямой, проходящей через две точки
. Для этого воспользуемся уравнением прямой, проходящей через две точки  .
.
В данном случае 
Из этого уравнения легко получаем  -
-
Это и есть уравнение прямой в отрезках на осях: параметр 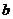 определяет точку пересечения прямой с осью
определяет точку пересечения прямой с осью  , параметр
, параметр  с осью
с осью  . Действительно, при х=0 получаем
. Действительно, при х=0 получаем  .
.
Вывести канонические уравнения прямой на плоскости,
|
|
|
Пусть  - плавающая точка прямой a. Тогда вектор
- плавающая точка прямой a. Тогда вектор 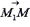 является направляющим вектором прямой a и имеет координаты
является направляющим вектором прямой a и имеет координаты  . Очевидно, что множество всех точек
. Очевидно, что множество всех точек  на плоскости определяют прямую, проходящую через точку
на плоскости определяют прямую, проходящую через точку  и имеющую направляющий вектор
и имеющую направляющий вектор  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 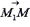 и
и  коллинеарны.
коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов 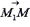 и
и  :
: 
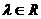 . Последнее равенство в координатной форме имеет вид
. Последнее равенство в координатной форме имеет вид 
Если  и
и  , то мы можем записать
, то мы можем записать

Полученное уравнение вида  называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy.
называют каноническим уравнением прямой на плоскости в прямоугольной системе координат Oxy.
Записать параметрические уравнения,
Уравнения системы  называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy.
называются параметрическими уравнениями прямой на плоскости в прямоугольной системе координат Oxy.
Вывести уравнение прямой, проходящей через две заданные точки.???????
Выведем уравнение прямой a, которая в прямоугольной декартовой системе координат Oxy проходит через две несовпадающие точки  и
и  .
.
Нам известно, что каноническое уравнение прямой на плоскости вида  задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку
задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку  и имеющую направляющий вектор
и имеющую направляющий вектор  .
.
Напишем каноническое уравнение прямой a, проходящей через две заданные точки  и
и  .
.
|
|
|
Очевидно, направляющим вектором прямой a, которая проходит через точки М1 и М2, является вектор  , он имеет координаты
, он имеет координаты 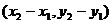 . Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора
. Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора 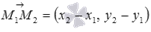 и координаты лежащей на ней точки
и координаты лежащей на ней точки  (и
(и  ). Оно имеет вид
). Оно имеет вид  (или
(или  ).
).

2.Правила дифференцирования: доказать формулу 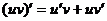 , перечислить остальные.
, перечислить остальные.
Докажем правило дифференцирования произведения двух функций.

Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что 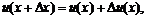
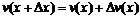 и
и
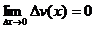 ,
,  (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
(приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
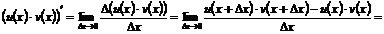

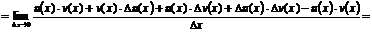




Что и требовалось доказать.
перечислить остальные правила дифференцирования
1) При дифференцировании константу можно выносить за производную: 
2) Правило дифференцирования суммы функций: 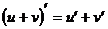
3) Правило дифференцирования разности функций: 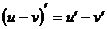
4) Правило дифференцирования частного функций: 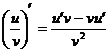 ,
, 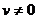
5) Правило дифференцирования функции в степени другой функции:
 ,
, 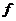 > 0
> 0
6) Правило дифференцирования сложной функции: 
7) Правило логарифма при дифференцировании функции:  ,
,  >0
>0
|
|
|
Билет 10 ????
1. Угол между прямыми на плоскости, если они заданы каноническими уравнениями или уравнениями с угловым коэффициентом (вывод)????.
Если прямые  и
и 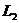 заданы каноническими уравнениями
заданы каноническими уравнениями  и
и  ,
,
где 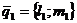 и
и 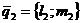 направляющие векторы прямых
направляющие векторы прямых  и
и 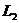 , то по аналогии получим:
, то по аналогии получим:  ,
,
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами  и
и  , вычисляется по формуле:
, вычисляется по формуле: 
Вывод
пусть даны:  и
и  и если углы наклона прямых к оси
и если углы наклона прямых к оси  соответственно равны
соответственно равны  и
и  , тогда:
, тогда:  ,
, 
Дата добавления: 2018-04-05; просмотров: 1096; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
