Вычисление определителя 3-го порядка разложением по элементам строки или столбца

Определителем третьего порядка называется следующее выражение:

Вычислить определитель 3-го порядка можно разложением

по элементам строки: ;

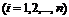и по элементам столбца: .

В этих формулах 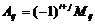- алгебраические дополнения элементов  матрицы , где — миноры элементов  матрицы .

Правило Саррюса

Дописывание двух первых строк или столбцов.

 

В этом случае считаем так:

Пример:

Вычислить определитель двумя способами: с помощью разложения по первой строке и по правилу треугольника:

Решение:

 1) с помощью разложения по первой строке:

2) по правилу треугольника:

    

Ответ: -21

Решение системы линейных уравнений 3-го порядка по правилу Крамера.

Рассмотрим систему 3-х уравнений с тремя неизвестными

Используя определители 3-го порядка, решение такой системы можно записать по правилу Крамера в следующем виде:   если D¹0.  Здесь

Вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

где x₁, x₂ – неизвестные переменные, a_{i j},  i = 1, 2, 3  j = 1, 2, 3 – числовые коэффициенты, b₁, b₂ b₃- свободные члены. Решением СЛАУ называется такой набор значений x₁, x₂, x₃   при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где - основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, 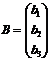- матрица – столбец свободных членов, а - матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x₁, x₂, x₃   матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.

Метод Крамера основывается на двух свойствах определителя матрицы:

2. Определитель квадратной матрицы ,   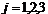равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
   

    

Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак, приступим к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А₁₁,  обе части второго уравнения – на А_{2 1,} обе части третьего уравнения – на А ₃₁ (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):

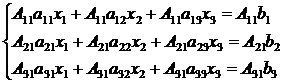
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x₁, x₂, x₃ и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем

 

и предыдущее равенство примет вид , откуда

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:
  

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x₁, x₂  и применяем свойства определителя:

Откуда                .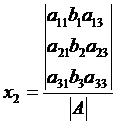

Аналогично находим x₃.

Если обозначить

,

то получаем формулы для нахождения неизвестных переменных по методу Крамера. , , .

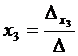Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:

Решение. Находим определитель основной матрицы системы

Поскольку D¹0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:

Тогда

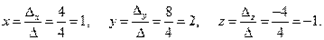
Проверка:

            Следовательно, решение найдено правильно.

2. Выпуклость: определение, признак выпуклости, точки перегиба.

Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

признак выпуклости:

Достаточный признак (выпуклости) вогнутости на интервале   :

Пусть функция y = f(x) имеет двойную производную во всех точках

Если <0 во всех точках интервала , то графиквыпуклый.

Если >0 всюду на интервале , то графиквогнутый.

точки перегиба:

Точкой перегиба графика функции  называется точка , в которой функция определена и которая разделяет промежутки выпуклости и вогнутости функции. В окрестности такой точки  график функции  слева и справа от точки имеет разные направления выпуклости. Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой – над нею. В окрестности тоски перегиба график функции геометрически переходит с одной сторон касательной на другую и «перегибается» через неё. Отсюда и произошло название «точка перегиба».

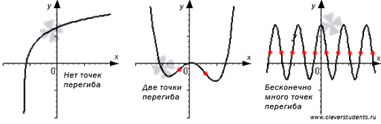
На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

 

Билет 3

1. Скаляры и векторы.

Скаляр - величина, каждое значение которой может быть выражено одним (действительным) числом без указания направления. Примерами скаляров являются длина, площадь, время, масса, плотность, температура и т. п.

Вектор - это величина, которая характеризуется своим численным значением и направлением.

---

Дата добавления: 2018-04-05; просмотров: 4573; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!