Релятивистік динамика элементтері 12 страница
9.3 Карноның идеал жылулық машинасы
Карно циклі деп тепе-теңдіктегі екі изотермиялық және екі адиабаталық ұлғаюлар мен сығылулардан тұратын қайтымды дөңгелек процесті айтады. Карноның идеал жылулық машинасы жылуоқшаулағыш төсенішке орнатылған жұмыс денесімен (газбен) толтырылған цилиндрден, температурасы 
қыздырғыштан және температурасы 
суытқыштан тұрады. Карно цикліне талдау жасайық.
1) Күй параметрлері 
, 
және 
(9.2–сурет, 
диаграммадағы 
нүкте) цилиндр ішіндегі газдың көлемін цилиндрді қыздырғышқа қойып, одан алынған 
жылу есебінен 
-ге дейін өте баяу, изотермиялық әдіспен өсіреді.
2) Цилиндрді жылуоқшаулағыш төсенішке қойып, газды адиабаталық түрде ұлғайтады. Газ 
жұмысты ішкі энергия есебінен жасайтындықтан, оның температурасы суытқыштың 
температурасына дейін төмендейді. 
қисығы газдың адиабаталық ұлғаюын сипаттайды.
3) Газдың сығылу процесі де екі сатылы жүреді. Алдымен жұмыс денесі орналасқан цилиндрді суытқышпен жалғастырып, изотермиялық әдіспен сығады. Газ  нүктемен белгіленген күйге жеткенде цилиндрді суытқыштан алып, жылуоқшаулағышқа қояды. Сығылу кезінде жасалған теріс жұмыс  жылуға айналып, суытқышқа беріледі.  қисығы газдың изотермиялық сығылуын сипаттайды.
4) Цилиндр жылуоқшаулағыш төсенішке қойылған соң, жұмыс денесін адиабаталық түрде одан әрі сығып, бастапқы  күйге қайта алып келеді.
| 
9.2 – сурет. Карно циклі
|
Бұл процесте газдың температурасы Т2 – ден Т1 – ге дейін өседі. 
қисығы газдың адиабаталық сығылу процесін сипаттайды. Температурасы қыздырғыштың бірдей болған газды қыздырғышпен қайта жалғап, циклді қайта бастайды.
Газдың бір циклде жасаған жұмысы 4.2 – суреттегі « 
» фигура ауданымен анықталады:
. (9.1)
Карно теоремасы
Жылулық қозғалтқыш циклінің үнемділігі жылулық пайдалы әсер коэффициенті (ПӘК немесе 
) арқылы сипатталады. Пайдалы әсер коэффициенті – бір циклде жасалған A жұмыс пен қыздырғыштан жұмыс денесіне берілген Q1 жылу мөлшерінің қатынасына тең физикалық шама. Карно циклі бойынша жұмыс істейтін қозғалтқыш үшін ПӘК:
. (9.2)
Бірқатар түрлендіруден соң Карно қозғалтқышының ПӘК-ін келесі түрге келтіруге болады:
. (9.3)
Соңғы екі формуладан келесі қатынасты табамыз:
. (9.4)
Олай болса, 
болғанда ғана 
болады. Бірақ температураны абсолюттік нөлге дейін төмендету мүмкін емес. Бұл Нернст теоремасы дәлелдеген термодинамиканың үшінші бастамасы. Сондықтан, әрқашан 
болады. Карноның жылулық машинасы – идеал жылу машинасы. Мұндағы барлық процестер өте баяу өтетіндіктен, оларды қайтымды процесс деп қарастыруға болады. Температурасы әртүрлі денелер бір-бірінен оқшауланған. Сондықтан жылуөткізгіштік арқылы энергия жоғалмайды. Нақты машиналардың жұмыс жасауы кезінде энергияның қайтымсыз жоғалуы әрқашан қатар жүретіндіктен, олардың пайдалы әсер коэффициенті Карно машинасының пайдалы әсер коэффициентінен әрқашан аз болады:
(9.5)
Жоғарыда келтірілген түсіндірмелер негізінде үш ережеден тұратын Карно теоремасы тұжырымдалады:
1) Карно циклінің 
қыздырғыш мен суытқыштың температурасына ғана тәуелді;
2) жұмыс денесіне тәуелі емес (идеал газдың күй теңдеуі белгілі болғандықтан, ол үшін 
есептеу жеңіл);
3) қайтымды цикл бойынша жұмыс істейтін машиналар ПӘК-i қайтымсыз цикл бойынша жұмыс істейтін машиналардың ПӘК-iнен әрқашан артық болады:
.
9.5 Клаузиус теңсіздігі
Карно теоремасына бойынша:
немесе 
.
Олай болса,
немесе 
.
Теңсіздіктің екі жағын 
бөлшегіне көбейтсек, келесі өрнектерді аламыз
немесе 
немесе 
,
Мұндағы 
– суытқышқа берілген жылу мөлшері; 
– жұмыс денесінің суытқыштан қабылдаған. Жүйенің қандай да бір денеден алған жылу мөлшерінің сол дененің температурасына қатынасын 
, Клаузиус, келірілген жылу мөлшері деп атады.
Соңғы теңсіздік Клаузиус теңсіздігі деп аталады. Оның физикалық мағынасы: жүйенің циклде сырттан алған келтірілген жылуының элементар мөлшерлерінің қосындысы қайтымды циклдер үшін нөлге тең, ал қайтымсыз циклдер үшін нөлден кіші болады:
. (9.6)
Энтропия
Жүйенің күйін аз шамаға өзгерту үшін оған қыздырғыштан берілетін элементар жылу мөлшері 
, ал қыздырғыштың температурасы Т болсын. Егер жүйедегі процесс қайтымды болу үшін, оның температурасы да Т болу керек. Қайтымды процесс кезіндегі келтірілген жылудың элементар мөлшерін dS арқылы белгілейік:
, (9.7)
мұндағы S – энтропия. Жылу мөлшері Q процесс функциясы. Ал, энтропия S күй функциясы болады.
9.6.1 Энтропияның қасиеттері
1) Энтропияның өзгеру сипаты бойынша жылуалмасу процесінің бағытын анықтауға болады. (9.7) өрнектен 
пен 
таңбалары бірдей болатынын көреміз. Олай болса, жүйеге жылу берілгенде (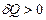 
) оның энтропиясы өседі ( 
); жүйеден жылу алынғанда (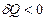 
) оның энтропиясы кемиді ( 
).
2) Оқшауланған жүйенің энтропиясы қайтымсыз процестер кезінде тек қана өседі, қайтымды процестер кезінде тұрақты болып қалады. Олай болса, оқшауланған термодинамикалық жүйенің энтропиясы ешқашан кемімейді:
. (9.8)
3) Қайтымды адиабаталық процестер изоэнтропты (мұндай процестерде энтропия өзгермейді)болады.
Карно циклі екі изотерма мен екі адиабатадан (изоэнтроптан) тұрады. Бұл процестің T-S диаграммасы (9.5 – сурет) қабырғалары координат өстеріне параллель тік төртбұрыш болады. 
формуласы бойынша, қыздырғыштан алынған жылу есебінен өтетеін 1 – 2 изотермиялық процесс кезінде жүйеге берілетін жылу мөлшері Q 1 тең болады:
, (9.9)
мұндағы S1 – жүйенің процесс басталар алдындағы энтропиясы, S2 – процесс соңындағы энтропия.
 9.5 – сурет. Карно цикліндегі жұмыс
| Изотермиялық 3 – 4 процесс кезінде суытқышқа берілетін Q2 жылу мөлшері тең болады:
 . (9.10)
Жүйенің бір циклде алатын жылу мөлшері
 ,(9.11) 9.5–суреттегі боялған тікбұрыштың ауданымен анықталады.
|
4) 9.1-кестеде идеал газдың әртүрлі процестерде 1 күйден 2 күйге өтулері үшін энтропияның өзгеру өрнектері келтірілген
9.1- кесте
Изохоралық
(  )
| Изобаралық
(  )
| Изотермиялық
(  )
| Адиабаталық
(  )
|
 ,
| 
| 
|
|
Бұл өрнектер
, (9.12)
формуладан шығады. Соңғы өрнек тепе-теңдікте процестердегі энтропия өзгерісін сипатайтын келесі формуладан алынған:
,
мұндағы 
, 
.
Өрнекті алу үшін 
және 
қатынастары қоланылды.
5) Жүйенің байланысқан энергиясы.
Қайтымды изотермиялық процесс кезінде жүйе жұмысты 
еркін энергия есебінен атқарады:
немесе
, (9.13)
мұндағы 
– жүйенің еркін энергиясы (Гельмгольц энергиясы). Мұндағы TS ішкі энергияның қайтымды изотермиялық процесс кезінде жұмысқа айнала алмайтын бөлігі. Ішкі энергияның бұл бөлігін байланысқан энергия деп атайды. Егер температура тұрақты болса, онда жүйенің энтропиясы артқан сайын оның байланысқан энергиясы да арта береді.
6) Энтропия – термодинамикалық жүйедегі күйлер ықтималдылығының өлшемі .
Жүйе күйлерінің термодинамикалық ықтималдылығы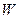 
осы күйдің жүзеге асырылу әдістерінің санымен анықталады. Басқаша айтқанда, белгілі макрокүй ықтималдылығы жүйенің осы күйін тудыратын барлық мүмкін микрокүйлер санына (микробөлшектердің жылдамдықтар мен координаталар бойынша жүйенің осы күйіне сәйкес келетін таралуы) тең. Термодинамикалық ықтималдылық W≥1, сондықтан ол бірден кіші болатын математикадағы ықтималдылықтан өзгеше.
Больцман жүйенің термодинамикалық ықтималдылығы 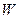мен энтропиясы 
арасында келесі тәуелділік бар екенін дәлелдеді:
. (9.14)
Бұл Больцман формуласы. Жүйенің қандай-да бір күйініің энтропиясы осы күйді тудыратын микрокүйлер санының логарифмімен анықталады.
9.7 Термодинамиканың екінші бастамасы
Термодинамиканың бірінші бастамасы энергияның сақталу және түрлену заңдарын сипаттағанымен, термодинамикалық процестердің жүру бағытын анықтауға мүмкіндік бермейді. Бұл бастама нәтижесі қандай да бір денеден алынған жылуды толығымен жұмысқа айналдыратын процестің мүмкіндігін жоққа шығармайды. Мысалы, термодинамиканың бірінші бастамасы бойынша белгілі жылу көзін суыту арқылы периодты жұмыс істейтін (мұхиттардың ішкі энергиясы есебінен) машина жасауға болады. Мұндай қозғалтқыш екінші текті мәңгі қозғалтқыш деп аталады.
Дата добавления: 2022-01-22; просмотров: 62; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!