Тема: Законы распределения вероятностей дискретных случайных величин
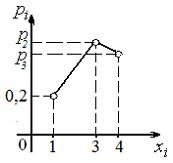
Закон распределения дискретной случайной величины X задан графически:
.
Известно, что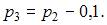 
Тогда значение 
равно …
| 1,4 | ||
| 1,8 | |||
| 1,6 | |||
| 1,35 |
Решение:
Графической формой представления закона распределения служит многоугольник распределения. В прямоугольной системе координат строят точки 
, которые соединяют отрезками прямых. Полученная фигура называется многоугольником распределения.
Равенство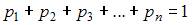 
позволяет найти неизвестное значение вероятности 
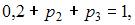отсюда 
По условию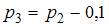 
, тогда 
то есть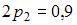 
и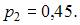 
Искомая вероятность 
Согласно рисунку,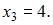 
В итоге имеем: 
Тема: Законы распределения вероятностей дискретных случайных величин
Игрок бросает игральную кость и получает 10 евро, если выпадает 5 очков, 100 евро, если выпадет 1 очко. В остальных случаях игрок не получает ничего. Закон распределения случайной величины 
– сумма, полученная игроком после броска игральной кости, имеет вид …
|
| 
| ||
| |||
| |||
|
Решение:
Законом распределения дискретной случайной величины называется соответствие между возможными значениями 
, 
, …, 
этой величины и соответствующими им вероятностями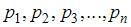 
:
,
где 
.
В задаче случайная величина – сумма, полученная игроком после броска игральной кости. Игрок может получить либо 0 евро, либо 10 евро, либо 100 евро в зависимости от выпавших очков. Поэтому 
, 
, 
. Определим вероятности для каждого из этих значений.
Игрок получит приз в зависимости от числа выпавших очков. Игральная кость имеет шесть граней, выпадение каждой из которых является равновероятным. Поэтому вероятность выпадения каждой грани равна 
.
Игрок получит 10 евро ( ), если выпадет 5 очков. Таким образом, вероятность получить 10 евро равна , то есть 
.
После выпадения 1 очка с той же вероятностью сумма выигрыша составит 100 евро, поэтому для имеем 
.
Во всех остальных случаях игрок ничего не выиграет: . Вероятность отсутствия выигрыша определим, исходя из условия 
, то есть 
. Отсюда 
.
Следовательно, случайная величина – количество очков, выпадающих при броске игральной кости, имеет следующий закон распределения
Тема: Законы распределения вероятностей дискретных случайных величин
Закон распределения вероятностей дискретной случайной величины имеет вид:
.
Тогда значение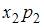 
равно …
|
| 
| ||
| |||
| |||
|
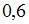
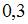
Решение:
Законом распределения дискретной случайной величины называется соответствие между возможными значениями этой величины и соответствующими им вероятностями
.
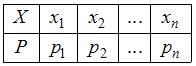Поскольку в результате испытания случайная величина примет одно из своих возможных значений, то события , , …, образуют полную группу событий и .
Из данного закона распределения имеем 
. Так как известны три вероятности из четырех, то для нахождения значения неизвестной вероятности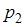 
будем использовать равенство 
. Имеем 
. Откуда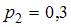 
. Следовательно, 
.
Дата добавления: 2018-02-15; просмотров: 711; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!