Тема: Числовые характеристики случайных величин. Математическое ожидание квадрата дискретной положительной случайной величины равно , а ее среднее квадратичное отклонение
Математическое ожидание квадрата дискретной положительной случайной величины  равно
равно  , а ее среднее квадратичное отклонение
, а ее среднее квадратичное отклонение  . Тогда математическое ожидание, вычисленное при помощи формулы для расчета дисперсии
. Тогда математическое ожидание, вычисленное при помощи формулы для расчета дисперсии  , равно …
, равно …

| 7 | ||
| 49 | |||
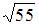
| |||

|
Решение:
Дисперсию случайной величины  можно вычислить при помощи формулы, указанной в условии:
можно вычислить при помощи формулы, указанной в условии:  . С другой стороны, средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии:
. С другой стороны, средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии:  . Поэтому
. Поэтому  . Подставив указанное выражение в первую формулу, получим:
. Подставив указанное выражение в первую формулу, получим:  .
.
Согласно условию,  ,
,  .
.
Отсюда имеем:  . Решая, получим
. Решая, получим  .
.
В итоге математическое ожидание может принимать значения  или
или  . Учитывая, что рассматривается случайная величина, принимающая только положительные значения, заключаем, что математическое ожидание также величина положительная.
. Учитывая, что рассматривается случайная величина, принимающая только положительные значения, заключаем, что математическое ожидание также величина положительная.
Таким образом, искомое значение  .
.
Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Плотность распределения непрерывной случайной величины имеет вид:  . Наименьшее значение, которое может принимать случайная величина
. Наименьшее значение, которое может принимать случайная величина  , равно …
, равно …

| 3 | ||
| 5 | |||
| 6 | |||
| 7 |
Решение:
Требуется определить наименьшее значение, которое может принимать случайная величина  . Напомним, что функция плотности распределения, согласно условию, имеет вид:
. Напомним, что функция плотности распределения, согласно условию, имеет вид:  , и для нее справедливо условие:
, и для нее справедливо условие:  , где
, где  – функция распределения случайной величины. При
– функция распределения случайной величины. При 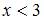 и
и 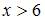 имеем
имеем  , то есть
, то есть  – некоторое число. Но, согласно свойствам функции распределения,
– некоторое число. Но, согласно свойствам функции распределения,  при
при 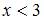 и
и 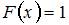 при
при 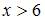 . Очевидно, что
. Очевидно, что  . Согласно определению, функция распределения
. Согласно определению, функция распределения  выражает вероятность того, что
выражает вероятность того, что  принимает значение, меньшее, чем
принимает значение, меньшее, чем  :
: 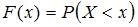 .
.
Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0. Таким образом, наименьшее значение, принимаемое случайной величиной, равно 3.
Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
График функции распределения непрерывной случайной величины имеет вид:

Тогда значение плотности распределения непрерывной случайной величины  при
при  равно …
равно …

| 0 | ||
| 1 | |||
| 0,5 | |||
| 2,5 |
Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Наибольшее значение, принимаемое непрерывной случайной величиной  , равно 3. Функция ее плотности распределения может иметь вид …
, равно 3. Функция ее плотности распределения может иметь вид …

| 
| ||

| |||

| |||

|
Решение:
Для плотности распределения непрерывной случайной величины  справедливо условие:
справедливо условие:  , где
, где  – функция распределения случайной величины. Согласно определению, непрерывная случайная величина
– функция распределения случайной величины. Согласно определению, непрерывная случайная величина  задается функцией распределения
задается функцией распределения  , выражающей вероятность того, что
, выражающей вероятность того, что  принимает значение, меньшее, чем
принимает значение, меньшее, чем  :
: 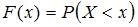 . Если
. Если  – наибольшее значение, принимаемое случайной величиной, то
– наибольшее значение, принимаемое случайной величиной, то  , поэтому
, поэтому  .
.
Таким образом, нас устраивает только такой вид  , который включает условие
, который включает условие  при
при  . Этому условию удовлетворяет функция:
. Этому условию удовлетворяет функция:  .
.
Заметим, что функция вида  не является плотностью распределения, так как не выполняется условие
не является плотностью распределения, так как не выполняется условие  при
при 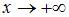 .
.
Функция вида  задает плотность распределения случайной величины
задает плотность распределения случайной величины  , наибольшее значение которой равно 2, так как выполняется условие
, наибольшее значение которой равно 2, так как выполняется условие  при
при  . Таким образом, она не удовлетворяет требованию задачи.
. Таким образом, она не удовлетворяет требованию задачи.
Верный ответ:  .
.
Дата добавления: 2018-02-15; просмотров: 818; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
