Тема: Теоремы сложения и умножения вероятностей
В первой урне 5 синих шаров и 2 желтых, а во второй – 7 синих и 3 оранжевых. Из каждой урны случайным образом извлекается 1 шар. Вероятность того, что вынуты оба шара одного цвета, вычисляется следующим образом …
| 
| ||
| |||
| |||
|
Решение:
Оба шара, вынутые из разных урн, могут иметь один и тот же цвет, если они синие.
Событие, состоящее в совместном появлении двух событий 
и 
, называется произведением событий 
и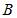 
.
Событие состоит в том, что из первой урны извлечен синий шар. Вероятность этого события, согласно условию, 
.
Событие состоит в том, что из второй урны извлечен синий шар.
Вероятность этого события, согласно условию, 
.
Событие 
– «из двух различных урн извлечены по одному шару одинакового цвета» – является произведением событий и .
События и являются независимыми, поскольку урны различны, и результат извлечения шара из первой урны не оказывает влияния на результат извлечения шара из второй урны. Тогда, согласно теореме о нахождении вероятности произведения двух событий, имеем: 
.
Тема: Теоремы сложения и умножения вероятностей
Вероятность утери ценной книги библиотечным фондом в течение первого года после ее выпуска составляет 0,2, а в течение второго календарного года 0,3. Тогда вероятность того, что книга будет сохранена фондом в течение двух лет, равна …
|
|
|
|
| 0,56 | ||
| 0,5 | |||
| 0,06 | |||
| 0,1 |
Решение:
Событие 
состоит в том, что книга будет утеряна в течение первого года после выпуска. Событие 
состоит в том, что книга будет утеряна в течение второго года. Согласно условию,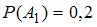 
, 
. Необходимо найти вероятность события – сохранности книги в течение двух лет, то есть вероятность того, что имели место одновременно события 
и 
, противоположные событиям, рассмотренным выше.
Вероятность события, противоположного данному, вычисляется по формуле 
. Имеем: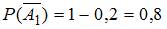 
, 
.
Событие, состоящее в одновременном появлении событий и , называется их произведением. Используя формулу вероятности произведения событий, получим: 
.
Тема: Теоремы сложения и умножения вероятностей
На стеллаже были выставлены 10-томное собрание сочинений Пушкина, три тома Дюма и 5 томов Лермонтова. Посетитель библиотеки наугад выбирает один из томов. Вероятность выбора произведения классика русской литературы равна …
|
| 
| ||
| |||
| |||
|
Решение:
Событие, состоящее в появлении хотя бы одного из событий и , называется суммой событий и . Вероятность суммы двух несовместных событий и вычисляется согласно формуле: 
.
Рассмотрим событие – наугад выбрано произведение классика русской литературы. Это может произойти в случае выбора тома Пушкина или книги Лермонтова. Пусть событие состоит в том, что выбрано произведение Пушкина, а событие состоит в том, что выбрано произведение Лермонтова. На полке 
книг. Таким образом, событие является суммой событий и . Согласно условию, произведения Пушкина составляют 10 книг из 18, а Лермонтова – 5 книг из 18. Поэтому 
, 
. События и являются несовместными, поскольку среди книг не было сборников произведений различных авторов. Тогда искомая вероятность равна: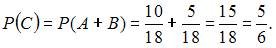 
|
|
|
Дата добавления: 2018-02-15; просмотров: 737; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!