Тема: Числовые характеристики случайных величин. Случайная величина задана законом распределения
Случайная величина 
задана законом распределения 
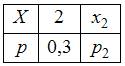. Ее математическое ожидание равно 
. Тогда значение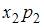 
равно …
| 
| ||
| |||
| |||
|
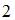
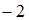
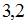
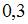
Решение:
Согласно определению, математическим ожиданием случайной величины с законом распределения
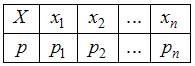
называется число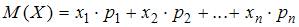 
.
Из условия имеем: , то есть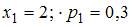 
.
Подставив в формулу для расчета математического ожидания случайной величины данные задачи, получим: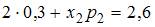 
.
Отсюда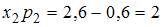 
.
Тема: Числовые характеристики случайных величин
Математическое ожидание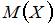 
случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью, равно …
|
| 4 | ||
| 16 | |||
| 8 | |||
| 1 |
Решение:
Согласно определению, математическим ожиданием случайной величины с законом распределения
называется число .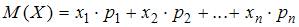
Составим закон распределения случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью (допустим,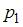 
):
.
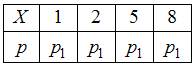Для определения значения 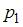воспользуемся формулой: 
.
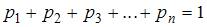В нашем случае 
. Отсюда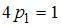 
, то есть 
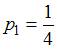. Таким образом, закон распределения случайной величины имеет вид:
.
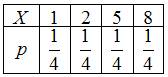Математическое ожидание случайной величины равно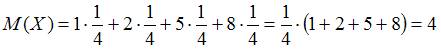 
.
Тема: Числовые характеристики случайных величин
Математическое ожидание дискретной случайной величины X, заданной законом распределения
,
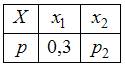где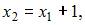 
равно 
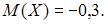Тогда значение 
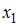равно …
|
|
|
|
| – 1 | ||
| 1 | |||
| 0 | |||
| – 2 |
Решение:
Согласно определению, математическим ожиданием случайной величины X с законом распределения
называется число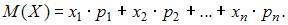 
Значение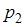 
найдем из условия 
то есть 
отсюда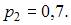 
Кроме того, учтем, что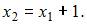 
Подставив в формулу для расчета математического ожидания случайной величины X данные задачи, получим: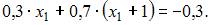 
Отсюда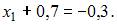 
В итоге имеем: 
Тема: Числовые характеристики случайных величин
Математическое ожидание 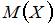случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью, равно …
|
| 4 | ||
| 16 | |||
| 8 | |||
| 1 |
Решение:
Согласно определению, математическим ожиданием случайной величины с законом распределения
называется число .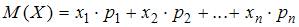
Составим закон распределения случайной величины, принимающей значения 1, 2, 5 и 8 с одинаковой вероятностью (допустим, ):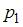
.
Для определения значения 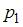воспользуемся формулой: .
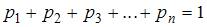В нашем случае . Отсюда 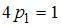, то есть 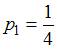. Таким образом, закон распределения случайной величины имеет вид:
.
Математическое ожидание случайной величины равно .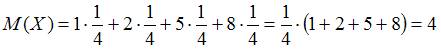
Тема: Числовые характеристики случайных величин
|
|
|
Математическое ожидание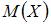 
случайной величины, заданной законом распределения
,
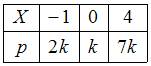равно …
|
| 2,6 | ||
| – 3 | |||
| 1 | |||
| 2,7 |
Решение:
Согласно определению, математическим ожиданием случайной величины X с законом распределения
называется число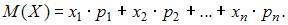
Определим значение k. Воспользуемся формулой: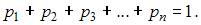 
В нашем случае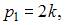 
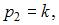
то есть 
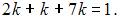Отсюда 
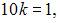в итоге 
Таким образом, закон распределения случайной величины имеет вид:
.
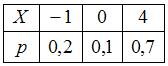Математическое ожидание случайной величины X равно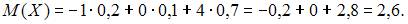 
Дата добавления: 2018-02-15; просмотров: 681; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!