Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Функция распределения непрерывной случайной величины X имеет вид:
Тогда значение плотности распределения 
при 
равно …
| 0 | ||
| 1 | |||
| 9 | |||
| 6 |
Решение:
Плотность распределения непрерывной случайной величины, согласно определению, является производной функции распределения результате дифференцирования: , где 
– функция распределения случайной величины.
Согласно условию, .
При имеем 
, так как 
.
Тогда 
.
Тема: Законы распределения вероятностей дискретных случайных величин
Закон распределения вероятностей дискретной случайной величины 
имеет вид:
,
а 
. Тогда значение 
равно …
|
| 
| ||
| |||
| |||
|
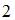
Решение:
Законом распределения дискретной случайной величины называется соответствие между возможными значениями этой величины и соответствующими им вероятностями
.
Поскольку в результате испытания случайная величина примет одно из своих возможных значений, то события 
, 
, …, 
образуют полную группу событий и 
.
Равенство будем использовать для нахождения значения неизвестной вероятности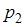 
. Имеем 
. Отсюда 
. По условию задачи , то есть 
, откуда имеем 
.
Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Функция распределения непрерывной случайной величины имеет вид:
. Тогда вероятность того, что случайная величина примет значение, меньшее 0,75, равна …
|
|
|
|
| 0,5 | ||
| 2 | |||
| 0,75 | |||
| 1,5 |
Решение:
Согласно определению, непрерывная случайная величина задается функцией распределения 
, выражающей вероятность того, что принимает значение, меньшее, чем 
: 
.
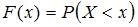Вероятность принятия случайной величиной значения, которое меньше 0,75, находится по формуле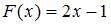 
, так как 
.
В итоге имеем: 
.
Тема: Законы распределения вероятностей дискретных случайных величин
Закон распределения дискретной случайной величины – количество выпадений «гербов» при двукратном подбрасывании монеты, имеет следующее графическое представление …
|
| 
| ||
| |||
| |||
| |||
Тема: Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
График функции распределения непрерывной случайной величины имеет вид:
.
Тогда значение, которое не может принимать случайная величина , равно …
|
| 1 | ||
| 6 | |||
| 7 | |||
| 9 |
|
|
|
Решение:
Согласно определению, непрерывная случайная величина задается функцией распределения , выражающей вероятность того, что принимает значение, меньшее, чем : .
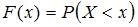Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0, поскольку это невозможно. Таким образом, мы должны рассмотреть все точки графика функции, для которых ордината (то есть значение функции) равна 0.
Эти точки образуют луч 
на оси абсцисс. При дальнейшем увеличении значения значение функции становится отличным от 0. Это значит, что принятие случайной величиной значений, меньших, чем 
, невозможно. Поэтому наименьшее из возможных значений, которые может принимать рассматриваемая случайная величина, равно 5. Очевидно, что из всех указанных значений этому условию удовлетворяет только 1.
Заметим, что вероятность того, что случайная величина примет значения, не большие 10, равна 1. Таким образом, случайная величина может принимать значения только в диапазоне от 5 до 10. Поэтому она может принимать значения 6, 7 и 9.
Дата добавления: 2018-02-15; просмотров: 794; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!