Тема: Классическое определение вероятности. В стопке из 16 конвертов на 7 приклеены марки
В стопке из 16 конвертов на 7 приклеены марки. Наудачу извлекают 2 конверта. Вероятность того, что на них не будет марок, равна …
| 
| ||
| |||
| |||
|
Решение:
Вероятностью события 
называется отношение числа элементарных исходов 
, благоприятствующих данному событию, к числу 
равновозможных элементарных исходов испытания: 
.
В данной задаче событие состоит в том, что из стопки конвертов выбраны наудачу два конверта без марок. Конвертов, которые не имеют марок, 
штук.
Вычислим . Определим, сколькими способами можно извлечь два конверта без марок ( 
) из девяти имеющихся ( 
). В этом нам поможет формула для нахождения числа сочетаний из 
элементов по 
: 
.
Имеем 
.
Теперь найдем . Определим, сколькими способами можно взять два конверта ( ) из имеющихся шестнадцати ( 
).
Получим 
.
Используя полученные значения, найдем вероятность события : 
.
Тема: Теорема сложения и умножения вероятностей
Вероятность поражения цели при выстреле для первого стрелка равна 0,4, а для второго – 0,5. Тогда вероятность того, что цель будет поражена после выстрелов обоих стрелков, равна …
|
| 0,7 | ||
| 0,9 | |||
| 0,2 | |||
| 0,1 |
Решение:
Рассмотрим событие 
– «цель поражена». Это значит, что хотя бы один из стрелков поразил цель. Таким образом, данное событие представляет собой сумму событий и 
, где событие – «первый стрелок поразил цель», событие – «второй стрелок поразил цель». Напомним, что суммой 
двух событий 
и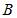 
называется событие, состоящее в появлении хотя бы одного из событий или 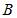, то есть или события , или события 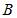, или обоих этих событий. Данные события являются совместными и независимыми, то есть они могут произойти одновременно (оба стрелка при выстреле могут поразить цель), и появление события не влияет на появление события 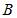(поражение цели первым стрелком не влияет на результат выстрела второго стрелка).
Поэтому, согласно теореме о сумме вероятностей для совместных событий, имеем: 
.
Следовательно, 
.
|
|
|
Тема: Теоремы сложения и умножения вероятностей
Вероятность того, что последняя цифра наугад набранного телефонного номера равна 3 или делится на 5, вычисляется следующим образом …
|
| 
| ||
| |||
| |||
|
Решение:
Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу элементарных исходов испытания:
.
Последняя цифра номера может являться любым числом от 0 до 9. Общее число элементарных исходов равно 
. Событие – «последняя цифра номера равна 3» – имеет единственный благоприятный исход: набрана цифра 3, то есть 
, вероятность 
.
Событие – «последняя цифра номера делится на 5» – имеет два благоприятных исхода: 0 и 5, а его вероятность 
.
Появление одного из этих событий исключает появление другого при одном испытании, значит, события и являются несовместными. Следует определить вероятность появления одного из этих событий, то есть вероятность суммы событий: 
.
Имеем: 
.
|
|
|
Дата добавления: 2018-02-15; просмотров: 809; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!