Тема: Основные понятия теории вероятностей. Свойства вероятностей. В урне лежат золотые, серебряные и медные монеты
В урне лежат золотые, серебряные и медные монеты. Наугад извлекается одна монета. Установите соответствия между случайными событиями и событиями, противоположными им:
1) «извлечена медная монета»
2) «извлечена золотая монета»
| 1 | «извлечена монета из драгоценного металла» | ||
| 2 | «извлечена медная или серебряная монета» | ||
| «извлечена монета из серебра» |
Решение:
Событие 
, состоящее из всех элементарных исходов, не входящих в событие 
, называется противоположным событием событию .
Для события – «извлечена медная монета» – противоположным является событие – «извлечена не медная монета», то есть золотая или серебряная. Данная формулировка может быть заменена следующей: «извлечена монета из драгоценного металла».
Для события 
– «извлечена золотая монета» – соответствующим противоположным является событие 
– «извлечена монета не из золота», то есть медная или серебряная.
Тема: Классическое определение вероятности
Из 3 карточек с цифрами 1, 2, 3 случайным образом собирают трехзначное число. Тогда вероятность того, что составленное число является четным, равна …
| 
| ||
| |||
| |||
|
Решение:
Вероятностью события называется отношение числа элементарных исходов 
, благоприятствующих данному событию, к числу 
равновозможных элементарных исходов испытания: 
.
Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов испытания.
Испытание состоит в том, что из 3 цифр случайным образом составляют трехзначное число. Все исходы испытания имеют одинаковую вероятность. Так как цифры не повторяются, то общее число элементарных исходов данного эксперимента равно количеству перестановок из 3 элементов, то есть 
.
Событие состоит в том, что составленное число является четным, то есть должно оканчиваться четной цифрой. Благоприятными исходами будут числа 132 и 312, то есть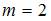 
. Следовательно, вероятность события равна 
.
|
|
|
Тема: Классическое определение вероятности
В урне 5 красных и 7 зеленых шаров. Из урны наудачу берут два шара. Вероятность того, что шары разноцветные, равна …
|
| 
| ||
|
| |||
| |||
|
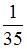
Решение:
Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания:
.
В данной задаче событие состоит в том, что из урны взяты два разноцветных шара, то есть 1 красный и 1 зеленый.
Вычислим . Определим, сколькими способами можно взять 1 красный и 1 зеленый шар из имеющихся. Существует 5 способов извлечения красного шара и 7 способов извлечения зеленого шара. Для каждого извлеченного красного шара существует 7 способов извлечения зеленого шара. Поэтому общее число способов, которыми можно извлечь 2 шара разных цветов, равно 
.
Теперь найдем . Определим, сколькими способами можно взять два шара ( 
) из имеющихся двенадцати шаров ( 
). В этом нам поможет формула для нахождения числа сочетаний из 
элементов по 
: 
. Получим 
.
Используя полученные значения, найдем вероятность события : 
.
|
|
|
Дата добавления: 2018-02-15; просмотров: 712; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!