Тема: Классическое определение вероятности. Студент забыл номер аудитории, в которой проходит занятие
Студент забыл номер аудитории, в которой проходит занятие. Он помнит только, что номер содержит три различных цифры, наибольшая из которых равна 5, а наименьшая равна 3. Вероятность того, что при случайном выборе он войдет в нужную дверь, равна …
| 
| ||
| |||
| |||
|
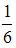
Решение:
Вероятностью события 
называется отношение числа элементарных исходов 
, благоприятствующих данному событию, к числу 
равновозможных элементарных исходов испытания: 
.
Из определения следует, что необходимо подсчитать число исходов, благоприятных данному событию, и число равновозможных элементарных исходов.
Очевидно, что благоприятное событие только одно, поскольку аудитория определена однозначно, то есть 
.
Общее число элементарных исходов – это количество чисел, которые можно составить из 3 различных неповторяющихся цифр. Поскольку номер содержит три различных цифры, наибольшая из которых равна 5, а наименьшая равна 3, то эти цифры: 3, 4 и 5. Используем формулу для подсчета перестановок 
.
Таких чисел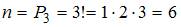 
.
Тогда вероятность того, что при случайном выборе будет найдена необходимая аудитория, равна 
Тема: Классическое определение вероятности
В урне 30 разноцветных шаров. Вероятность извлечь наугад один синий шар равна 0,6. Тогда количество синих шаров в урне равно …
|
| 18 | ||
| 5 | |||
| 12 | |||
| 50 |
|
|
|
Решение:
Вспомним определение вероятности. Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания:
.
Событие состоит в том, что из урны извлечен синий шар. Вероятность этого события 
. Общее число равновозможных элементарных исходов равно количеству шаров в урне, то есть 
.
Из определения вероятности получаем 
. Откуда 
. Мы получили число элементарных исходов испытания, благоприятствующих событию , то есть количество синих шаров в урне. Следовательно, в урне 18 синих шаров.
Тема: Классическое определение вероятности
Бросают 2 игральные кости. Вероятность того, что выпадет не менее 11 очков, равна …
|
| 
| ||
| |||
| |||
|
Решение:
Вероятностью события называется отношение числа элементарных исходов , благоприятствующих данному событию, к числу равновозможных элементарных исходов испытания: .
Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов.
Вычислим число благоприятных исходов. При броске 2 игральных костей может выпасть не менее 11 очков, то есть выпадет 11 или 12 очков. Это возможно в следующих случаях: когда на 2 костях одновременно выпадет по 6 очков (всего 12 очков), когда на первой кости выпадет 5 очков, а на второй – 6 (всего 11 очков) или когда на первой кости выпадет 6 очков, а на второй – 5 (всего 11 очков). Следовательно, 
.
Общее число элементарных исходов определим, исходя из следующих рассуждений. Пусть на первой кости выпало 1 очко. На второй может выпасть 1, 2, 3, 4, 5 или 6 очков. Таким образом, для каждой выпавшей грани одной игральной кости может выпасть одна из 6 граней на другой. Поэтому общее число исходов определяется формулой: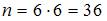 
. Итак, 
.
|
|
|
Дата добавления: 2018-02-15; просмотров: 889; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!