Исследовать ряд на сходимость

.

 -

расх-ся, т.к. расх-ся ряд .

По признаку сравнения  расходится.

 

25Найти кривизну кривой   в точке .

Найти под каким углом пересекаются линии   на прямом геликоиде

Решение:

Кривизна k= ;

 

k= =

 

 

 

 

Билет 26

26Делимость в кольце целых чисел ……

Делимость в кольце целых чисел.Целое число b делит целое число a, если существует q такое, что a = bq. b – делитель числа a, a – кратно числу b, q –частное.

В этом случае говорят, что , a делится на b (a : b), либо b делит a (b | a).

Лемма 1:Для любых a, b, c справедливы следующие свойства:

1) Если a ¹ 0, то a | a.

2) Если a | b, b | c., то a | c.

3) Если a | b, то a | -b, -a | b, -a | -b, |a| | |b| (|a| - модульчисла a).

4) Если a | b и a | c, то для любых u и vÎZÞa | (bu+cv).

5) Если a¹ 0, то a | 0.

6) 1 | a.

7) Если a | b и b¹ 0, то |a| £ |b|

Деление с остатком.Опр:Разделить число а на число b¹ 0 с остатком означает найти два таких числа q и r, чтобы выполнялось a = bq + r, r³ 0, r< |b|, где q – неполное частное, r – остаток от деления. r = 0 Ûb | a .

Т-ма 1.Для любого числа а и любого числа b¹ 0 существуют и притом единственные числа q и r такие, что a = bq + r, 0 £r< |b|

Док-во:1) Существование:

a) Пусть b> 0. Составим числа кратные b и расположим их в порядке возрастания. …< -2b< -b< 0 <b< 2b< 3b<…. существует такое число q, что bq£a<b(q+1)  

0 £ a - bq < b, т.е. r = a – bq, a = bq + r, где 0 £ r < b = |b|

b) Пусть b< 0, то - b> 0.  Для числа a и (- b) из пункта (а) следует, что существуют числа q и rÎZ      такие, что a = -bq + r, 0 £r< |-b|, тогда a = b(-q) + r, 0 £r< |-b| = |b|,

2) Единственность: Предположим,что числа q и r не единственные, т.е.

a = bq₁ + r₁ = bq₂ + r₂, т.е. b(q₁ – q₂) = r₂ - r₁ Þb | (r₂ - r₁).

Возможно: а) r₂ - r₁ = 0 Þr₂ = r₁ Þq₁ – q₂ = 0 Þq₁ = q_2.

b) r₂ - r₁¹ 0 Þ по лемме 1 |b| £ | r₂ - r₁| (1)

Т.к. r₂ и r₁ – остатки, то 0 £r₁< |b|, 0 £r₂< |b| Þ   | r₂ - r₁| < |b| (2)

Имеем:(1)противоречит(2).Полученное противоречие говорит о том, что такого случая быть не может. Значит r₂ = r₁ и q₁ = q₂.

НОД:Всякое целое число, которое делит числа a и b называется их общим делителем. Наибольший из общих делителей наз-ся наибольшим общим делителем НОД(a,b).

Cвойства НОД:

1) НОД(a,b) > 0 2)НОД(a,0) = |a| 3)НОД(0,0) не существует 4)НОД(a,b) = НОД(-a,-b) Þ при рассмотрении НОД(a,b) мы можем брать неотрицательные числа a и b.

Лемма 2.Если a | b, то НОД(a,b) = |a|.

Док-во:Если c | a, то по лемме 1 с | bÞ любой делитель числа а яв-ся делителем числа b, поэтому все делители числа а составляют множество общих делителей a и b, тогда самый большой делитель = |a|.

Лемма 3. Для любых целых чисел a, b, c¹ 0, для к-рых выполняется a = bq + c справедливо НОД(a,b) = НОД(b,c).

Док-во:Пусть m – общий делитель чисел a и bÞm | a, m | bÞ по лемме 1 m | (a-bq),

a-bq = cÞm | cÞm общий делитель чисел b и с. Пусть m – общий делитель чисел b и с. Þm | b и m | с Þm | (bq+с), Þm | aÞm - общий делитель a и b. Таким образом мн-во общих делителей a и b совподает с мн-твом общих делителей с и bÞ наибольший элемент мн-тва совподает с НОД(a,b) и НОД(b,c), поэтому НОД(a,b) = НОД(b,c).

Алгоритм Евклида и его приложения.

Пусть a, bÎZ, b¹ 0, тогда: если b | a, то НОД(a,b) = |b|.

Пусть b не делит a, тогда a = bq₁ + r₁, 0 <r₁< |b|,

b = r₁q₂ + r₂, 0 < r₂< r₁,

                                       r₁ = r₂q₃ + r₃, 0 < r₃< r₂,

                                       …………………………..

                                       r_n-2 = r_n-1q_n + r_n, 0 < r_n< r_n-1,

                                       r_n-1 = r_nq_n+1

Имеем: |b| > r₁ > r₂ >….> r_n-1. Т.к. остатки уменьшаются и ограничены снизу 0, то цепочка конечна.

Теорема 2:Пусть a, bÎZ, b¹ 0, тогда: если b | a, то НОД(a,b) = |b|, если b не делит a, то НОД(a,b) равен последнему ненулевому остатку в алгоритме Евклида.

Док-во: Пусть b не делит a, тогда по лемме 3

НОД(a,b) = НОД(b, r₁) = НОД(r₁, r₂) = …= НОД(r_n-2, r_n-1) = НОД(r_n-1, r_n) = r_n.

Теорема 3(о линейном выражении НОД черех исходные числа): Пусть a, bÎZ, a³ 0, b³ 0.

Пусть cуществует НОД(a,b), тогда cуществуют целые числа u и v такие, что НОД(a,b) = ua + vb.

Док-во: Пусть m = НОД(a,b)

1) Пусть a = 0 Þ b ¹ 0, тогда НОД(a,b) = НОД(0,b) = b = 0a + 1b.

2) Пусть b = 0 Þ a ¹ 0, тогда НОД(a,b) = НОД(a,0) = a = 1a + 0b.

3) Пусть a ¹ 0, b ¹ 0. Т.е. a > 0, b > 0.

Дальнейшее док-во проведем методом мат.индукции по числу строк в алгоритме Евклида.Пусть в алгоритме Евклида одна строка, тогда a = bq₁ÞНОД(a,b) = b = 0a + 1b.  Утве-ние выполняется. Предположим, что утверждение верно для любых целых чисел, у которых в алгоритме Евклида £n строк. Докажем, что утверждение верно при количестве строк = n+1. Будем рассматривать алгоритм без первой строки. Оставшиеся n строк являются алгоритмом Евклида для чисел b и r₁. Т.к. в этом алгоритме n строк, то утверждение для b и r₁ верно. Þcуществуют целые числа u₁ и v₁ такие, что НОД(b,r₁) = u₁r₁ + v₁b.

НОД(b,r₁) = r_n = НОД(a,b) = u₁r₁ + v₁b = u₁(a - bq₁) + v₁b = u₁a - u₁q₁b + v₁b

= u₁a + (u₁q₁ - v1)b = ua + vb. Cогласно принципа мат.индукции утверждение теоремы верно для целых чисел с любым числом строк в алгоритме Евклида.

Взаимно простые числа.

Два целых числа наз-ют взаимно простыми, если их НОД равен 1.

Лемма 4. Если a | bc и НОД(a,b) =1, то a | c.

Док-во: Т.к. НОД(a,b) =1, то по теореме 3 то по т-ме 3 cущ-ют целые числа u и v такие, что 1 = ua + vb. Умножим на с: c = uac + vbc.

uac : a (uac делится на а) и vbc : a (uac делится на а). Т.к. a | bc Þ по лемме 1 c : a или a | c.

Теорема 4. Целые числа a и b взаимно просты Û когда сущ-ют целые числа u и v такие, что 1 = ua + vb.

Док-во: 1)Пусть a и b взаимно просты Þ НОД(a,b) =1 Þ по т-ме 3 сущ-ют целые 

числа u и v такие, что 1 = ua + vb.2)Пусть сущ-ют целые числа u и v такие, что 1 = ua + vb. Пусть НОД(a,b) = с Þ с | a и c | bÞ по лемме 3 с | (a + vb) = c | 1 Þc = 1

НОК. Если сÎZ, с делится на а и с делится на b, то с – общее кратное чисел а и b. Наименьшее полож-ное число в мн-ве общих кратных чисел а и b наз-ся наименьшим общим кратным чисел а и b. НОК(0,b) не существует.

Т-ма 5(связь НОК и НОД) Для любых a , b> 0, a , bÎZ верно: ab = НОД(a,b)НОК(a,b)

Док-во: Пусть с = НОД(a,b) Þ с | a и a = ca₁, c | b и b = cb₁ Þ НОД(a₁,b₁) = 1.

m – общее кратное Þa | m и b | m, тогда m = ак = сa₁к Þb | сa₁к Þcb₁ | сa₁к Þ

b₁ | a₁к Þ по лемме 4 b₁ | к Þ к = b₁l, lÎZÞm = ca₁b₁l. Т.к. в последнем произведении может менятся только l, то m будет НОК, если l = 1. НОК(a,b) = ca₁b₁l = (ca₁сb₁) / c = ab / c = ab / НОД(a,b) Þ ab = НОД(a,b)НОК(a,b)

Простые числа. Целое число p>1 наз-ся простым, если оно не имеет других полож-ных делителей, кроме 1 и p. Все целые числа >1 отличные от простых чисел наз составными.

Лемма 5. Всякое натуральное число n> 1 делится хотя бы на одно простое число.

Т-ма 6(Евклида). Мн-во всех простых чисел бесконечно.

Док-во: От противного: пусть p₁, p₂,…, p_k.- все простые числа, тогда Рассмотрим

q = 1 + p₁p₂…p_kq>p_i для любого i = 1, 2, .., k. q – составное, по лемме 5 число q делится хотя бы на одно простое число, например p₁ , p₁ | q, p₁ | q и p₁ | p₁p₂…p_kтогда p₁ | (q - p₁p₂…p_k), т.е. p₁ | 1 Þp₁ = 1. Противоречие.

Лемма 6. Если nÎN, p – простое, то либо р делит n, либо р и n взаимно просты.

Лемма 7. Если произведщение нескольких натуральных чисел делится на простое число, то хотя бы один из множителей делится на это простое число.

Теорема 7.Всякое натуральное число >1 либо является простым, либо представимо в виде произведения простых единственным образом

Каноническое разложение числа. Пусть в разложении а ÎZ в произведении простых множителей число р₁ встречается a₁ раз, р₂ встречается a₂ раз,…,р_n встречается a_n раз, тогда

Т-маПусть 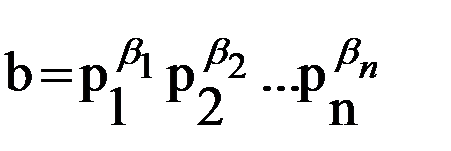. Тогда 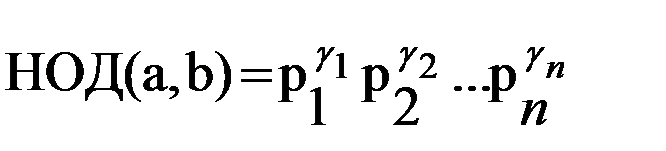Где g_i = min{a_i,b_i} i =1, 2, … n

Гдеg_i = max{a_i,b_i} i =1, 2, … n.

---

Дата добавления: 2018-02-15; просмотров: 527; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!