Теорема об изменении кинетической энергии точки.
Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
 Доказательство: Основной закон динамики
Доказательство: Основной закон динамики  .Умножим левую и правую части уравнения скалярно на
.Умножим левую и правую части уравнения скалярно на 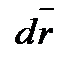 справа, получаем
справа, получаем  .
.  - элементарная работа.
- элементарная работа.
 - дифференциал от кинетической энергии.
- дифференциал от кинетической энергии.
 , что и требовалось доказать.
, что и требовалось доказать.
Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.

Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.

Написать ряд Фурье функции
 на отрезке
на отрезке 

Т.к. f(x) – периодичная функция, то
воспользуемся тригонометрическим рядом Фурье.
 ,
,
 ,
, 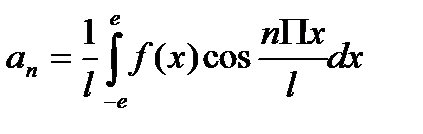 ,
,  .
.
Получаем:
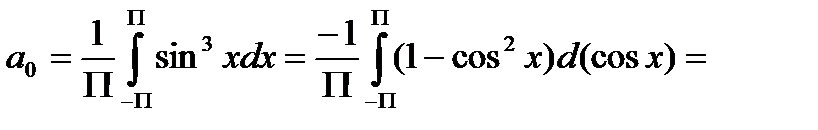

 .
.
 , т.к. для нечёт.
, т.к. для нечёт.


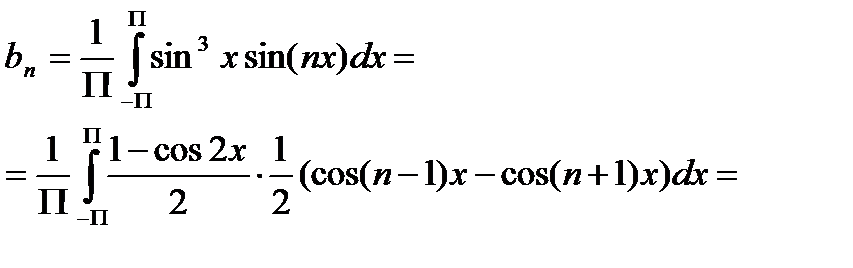




 .
.
При n = 1: 
При n = 3: 
След-но,  27Пусть m – мера Лебега на
27Пусть m – мера Лебега на  R. Найти
R. Найти  , где D(x) – функция Дирихле,
, где D(x) – функция Дирихле,
 - характеристическая функция множества А.
- характеристическая функция множества А.
Решение:
 Þ
Þ 
Т.о. на [0,4] f(x) простая измеримая. Зн., 
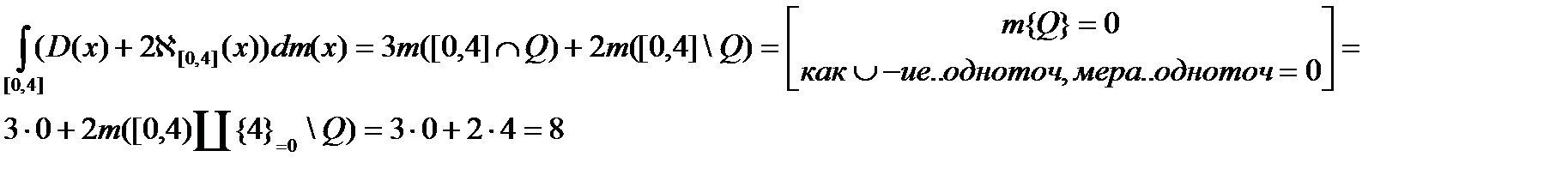 Т.к. m(QÇ[0,4])=m(Q)+m([0,4])-m(QÈ[0,4])=m(Q)+m([0,4])- m([0,4])=m(Q)=0
Т.к. m(QÇ[0,4])=m(Q)+m([0,4])-m(QÈ[0,4])=m(Q)+m([0,4])- m([0,4])=m(Q)=0
m([0,4]\Q)=m([0,4])-m([0,4] ÇQ)==m([0,4])=m([0,4))=4-0 + m({4})=0 =4-0+0=4
m({4})=0, т.к. {4}=  Þm({4})=
Þm({4})=  Ответ: 8
Ответ: 8
Билет 28
28Определители (ф-ла определителя квадратной матрицы; вычисление опр-лей малых порядков; вычисление опр-ля разложением по строке (столбцу); теорема об опр-ле произведения матриц; обратимые матрицы; вычисление обратной матрицы с помощью алгебраических дополнений).
|
|
|
О: Пусть k,l  N,
N,  - матрицей над полем P, будем называть совокупность элементов поля P, записанную в виде прямоугольной таблицы. А=
- матрицей над полем P, будем называть совокупность элементов поля P, записанную в виде прямоугольной таблицы. А=  .
.
Будем рассматривать только квадратные матрицы.
Пусть А={a  }- квадратная матрица.
}- квадратная матрица.
О: Определителем или детерменантом матрицы А называется число, которое обозначается |A| или detA и вычисляется по формуле detA=  .
.
О: Пусть А- квад-я матрица порядка n . Матрица А называется обратимой, если существует матрица В квад-я матрица порядка n, т.что АВ=ВА=Е – в этом случае матрица В наз-ся обратной для матрицы А и обозначается А  .
.
Вычисление обратной матрицы.
Теорема 1: Обратную матрицу А с помощью элементарных преобразований можно превратить в единичную, применяя те же элементарные преобразования в том же порядке из единичной матрицы получим обратную для матрицы А. (А|Е)=(Е| А  ).
).
Теорема 2: Квадратная матрица А обратима т.т.т., когда она невырождена причем если матрица А невырождена, то
А 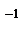 =
= 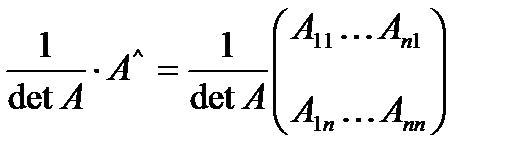 , где
, где  =(-1)
=(-1)  - алгебраическое дополнение,
- алгебраическое дополнение,  -минор для элемента
-минор для элемента  -называется определитель матрицы полученной из матрицы А вычеркиванием i-строки, j- столбца.
-называется определитель матрицы полученной из матрицы А вычеркиванием i-строки, j- столбца.
Уравнение Лагранжа второго порядка для с-мы материальных точек
Общее уравнение динамики сис. мат. точек в обобщённых координатах имеет вид: δq1 (δ/ δt *( δT/ δq1) – δT/ δq1 -Q1) + δq2(δ/ δt - δT/ δq2 – δT/ δq2 – Q2) + … + δqS(δ/ δt - δT/ δqS – δT/ δqS - QS) = 0
|
|
|
Где q1, q2,…, qS – обобщённые координаты, q1, q2,…, qS - обобщённые скорости, δq1, δq2,…, δqS - обобщённые возможные перемещения системы явл. вариациями соотвств. обобщ. координат,
Q1, Q2,…, QS - обобщ. силы системы, Т – кин. энергия системы. Т.к. δq1, δq2,…, δqS в случае системы, подчиненной голомным связями, явл. независимыми обобщ. возможн. перемещ., то общ. ур–е динамики удовлетворяет лишь при условии, что коэф., стоящие при возможных перемещениях = 0, т.е.
δ/ δt *( δT/ δq1) – δT/ δq1 = Q1 } – уравнение Лагранжа 2 рода.
δ/ δt *(δT/ δq2) – δT/ δq2 = Q2 }28Проверить, является ли последовательность  точек метрического пространства С[0;1] сходящейся, фундаментальной.
точек метрического пространства С[0;1] сходящейся, фундаментальной.
Решение:
Последовательность будет функциональной. Если она будет сходится.
Докажем сходимость:
Последовательность {xn} метрич. пр-ва Х сх-ся в Х, если $х0ÎХ : "e$NeÎN : "n³Ne
g(xn,x0)<e.
{xn}= 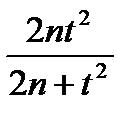 g(x,y)=
g(x,y)=  пусть х0(t)=1, тогда
пусть х0(t)=1, тогда 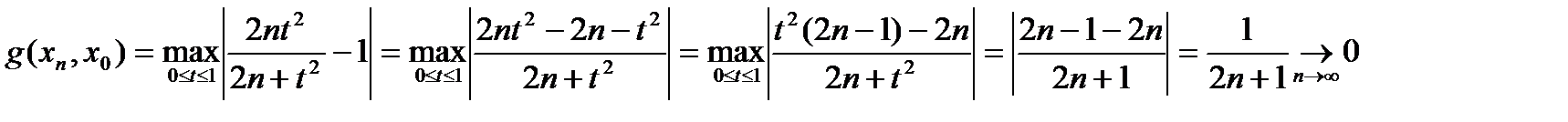
Þ {xn}-сх-ся.
Þфундаментальна Ответ:явл-ся.
28Приведите уравнения к каноническому виду:

Решение:

Билет 29
29Непрерывные функции. Свойства функций, непрерывных на отрезке.
|
|
|
Опр. Пусть f определена в некоторой окрестности точки x0, f наз непр в т. x0, если  . По Гейне: какую бы ни взять (xn)
. По Гейне: какую бы ни взять (xn)  x0, соответствующая посл-ть значений f(xn)
x0, соответствующая посл-ть значений f(xn)  f(x0). По Коши:
f(x0). По Коши:  >0
>0  >0
>0  удовлетворяющих неравенству
удовлетворяющих неравенству  имеем
имеем 
Пусть f задана на отрезке [a;b], f наз непр на отрезке, если f непрерывна во всех точках из интервала (a;b), непр справа в точке a и непр слева в точке b.
Т(Вейерштрасса): Если f(x) непрерывна на отрезке [a;b], то f(x) ограничена на отрезке [a;b] и достигает на нем своей точной верхней и нижней грани.
Доказательство: (от противного) Пусть f не ограничена на [a;b], пусть например f неограничена сверху, тогда можно говорить, что supf(x)=+  (sup всех чисел которые могут быть получены при x
(sup всех чисел которые могут быть получены при x  [a;b])
[a;b]) 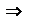
 x1
x1  [a;b]: f(x1)>1,
[a;b]: f(x1)>1,  x2
x2  [a;b]: f(x2)>2,
[a;b]: f(x2)>2,  ,
,  xn
xn  [a;b]: f(xn)>n,
[a;b]: f(xn)>n,  Имеем последовательность (xn) точек отрезка, то
Имеем последовательность (xn) точек отрезка, то  сходящящаяся последовательность
сходящящаяся последовательность 
 с другой стороны f непрерывна в x0,
с другой стороны f непрерывна в x0, 
 x0 и следовательно
x0 и следовательно  . Доказана ограниченность f на отрезке [a;b]. Докажем, что f достигает своей точной верхней грани; обозначим
. Доказана ограниченность f на отрезке [a;b]. Докажем, что f достигает своей точной верхней грани; обозначим  .
.  x1
x1  [a;b]: f(x1)>M-1,
[a;b]: f(x1)>M-1,  x2
x2  [a;b]: f(x2)>M-
[a;b]: f(x2)>M-  ,
,  ,
,  xn
xn  [a;b]: f(xn)>M-
[a;b]: f(xn)>M- 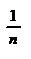 ,
,  (xn) последовательность точек отрезка
(xn) последовательность точек отрезка  сходящаяся подпоследовательность
сходящаяся подпоследовательность  ;
; 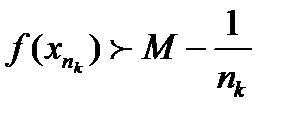 ; M-
; M-  <
<  при
при 


Т(Больцано-Коши)Если f непр на [a;b] и на концах его принимает знач равных знаков, то 
|
|
|
Т(Больцано-Коши. О промежуточном значении)
Если f непрерывна на отрезке [a;b], то для любого с лежащего между f(a) и f(b), то  c
c  [a;b]: f(c)=c; т.е.f принимает все промежуточные значения от f(a) до f(b).
[a;b]: f(c)=c; т.е.f принимает все промежуточные значения от f(a) до f(b).
Доказательство. Пусть f(a)<f(b, рассмотрим ф-wb.  ,
,  ,
,  , по пред теореме
, по пред теореме  т. с
т. с  [a;b]:
[a;b]:  ,т.е. f(c)=с.
,т.е. f(c)=с.
С-мы л-ных у-ний (совместные, несовместные и равносильные системы; критерий совместности системы линейных уравнений (теорема Кронекера-Капелли); крамеровская система; правило Крамера и матричный метод решения крамеровских систем; однородная система линейных уравнений; условия существования ненулевого решения однородной системы линейных уравнений).
Опр. Сис-мой k линейных у-ий c m неиз-ными  наз-ся совокупность у-ний вида
наз-ся совокупность у-ний вида  Числа aij наз-ся коэф-тами системы, числа bi – свободные члены системы, числа aij и bi выбираются из некоторого фиксированного поля P.Решением системы наз-ся совокупность элементов
Числа aij наз-ся коэф-тами системы, числа bi – свободные члены системы, числа aij и bi выбираются из некоторого фиксированного поля P.Решением системы наз-ся совокупность элементов  из поля P при подстановке к-рых в у-ния с-мы вместо
из поля P при подстановке к-рых в у-ния с-мы вместо  каждое из у-ний обращается в верное равенство. Решить систему у-ний значит найти все её решения или док-ть, что их нет. Опр. Сис-ма линейных у-ний имеющая хотя бы одно решение наз-ся совместной. Сис-ма, не имеющая ни одного решения наз-ся несовместной.
каждое из у-ний обращается в верное равенство. Решить систему у-ний значит найти все её решения или док-ть, что их нет. Опр. Сис-ма линейных у-ний имеющая хотя бы одно решение наз-ся совместной. Сис-ма, не имеющая ни одного решения наз-ся несовместной.
Матрица 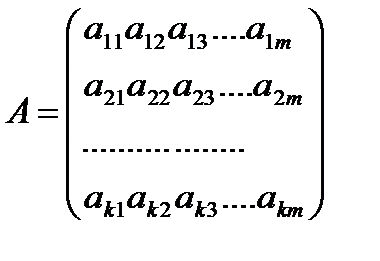 составленная из коэф-тов ур-ий системы называется матрицей системы линейных ур-ний. Если к матрице A добавить столбец свободных членов , то получим :
составленная из коэф-тов ур-ий системы называется матрицей системы линейных ур-ний. Если к матрице A добавить столбец свободных членов , то получим : 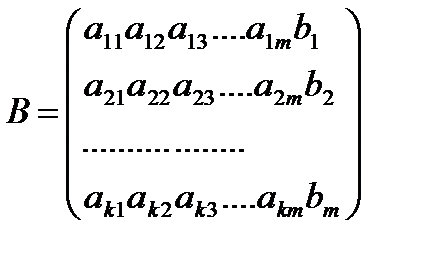 , если обозначить через
, если обозначить через  матрицу из неизвестных эл-ов, а через
матрицу из неизвестных эл-ов, а через  - матрицу из свободных членов, то систему линейных ур-ний можно записать в виде матричного ур-ния: A*X=C. Эта запись наз-ся матричной записью системы линейных у-ний.
- матрицу из свободных членов, то систему линейных ур-ний можно записать в виде матричного ур-ния: A*X=C. Эта запись наз-ся матричной записью системы линейных у-ний.
Опр Элементарными преобразованиями сис-мы линейных ур-ний системы будем наз-ть следующие преобразования:
1. Умножение какого – либо ур-ния на ненулевое число
2. Прибавление к одному уравнению второго у-ния системы, умноженного на некоторое число.
Опр Две системы линейных уравнений от одних и тех же переменных наз-ся равносильными, если каждое решению первой системы яв-ся решением второй системы и наоборот, или же если обе системы несовместны.
Имеют место следующие теоремы
Т-ма 1.При элементарных преобразованиях система переходит в равносильную ей систему.
Опр. Сис-ма линейных у-ний наз-ся ступенчатой если её расширенная матрица яв-ся ступенчатой.
Т-ма 2. Всякую систему линейных у-ний можно привести к ступенчатой сис-ме с помощью элементарных преобразований
Опр. Пусть дана сис-ма линейных у-ий  (1)
(1)
Эту систему (1) можно записать в виде матричного у-ния AX=B, где  ,
,  ,
, 
Система линейных у-ний наз-ся крамеровской сис-мой если выполняется два условия:
1. Число у-ний равно числу неизвестных
2. Det (определитель) матрицы системы ¹ 0
Т-ма 3 . Крамеровская система имеет единственное решение 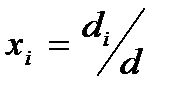 , i=1,2,3,…..,k
, i=1,2,3,…..,k
где d –определитель матрицы системы, di опр-ль матрицы, у которой в i-ом столбце стоят свободные члены b1 ,b2 ,b3 , … ,bк , все остальные столбцы как у матрицы системы.
Док – во Пусть система (1) крамеровская. Тогда k = m и detA¹0, тогда сущ-ет матрица обратная A – A-1. Заметим, что система (1) и матричное у-ние AX=B (2) равносильны.
Покажем, что матричное у-ние (2) имеет еди-ное реш-ие.
Умножим обе части (2) слева на A-1 . Получим A-1(AX)=A-1B, X=A-1B. Таким образом система (1) имеет решение 

 Тогда Xi=
Тогда Xi= 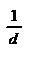 (A1ib1+ A2ib2+…+ Akibk)=
(A1ib1+ A2ib2+…+ Akibk)=  , i=1,….,k
, i=1,….,k  Теперь докажем что решение крамеровской сис-мы единственное
Теперь докажем что решение крамеровской сис-мы единственное
Пусть X1 и X2 два решения крамеровской сис-мы. Тогда AX1=B и AX2=B Отсюда X1=X2
Т-ма 4 (Кронекера-Капелли) Для того чтобы сис-ма линейных у-ий была совместна необх-мо и дос-но чтобы ранг матрицы сис-мы был равен рангу расширенной матрицы.
Док – во. 1 НЕОБХОДИМОСТЬ. Пусть сис-ма  (1)
(1)
совместна и  решение сис-мы. Тогда
решение сис-мы. Тогда

………………………….
 (2)
(2)
Выпишем расширенную матрицу системы  Матрица системы это матрица
Матрица системы это матрица  Преобразуем матрицу B с помощью элементарных преобразований следующим образом. От последнего столбца отнимем i-й столбец умноженный на ci (для всех i от 1 до m). Получим:
Преобразуем матрицу B с помощью элементарных преобразований следующим образом. От последнего столбца отнимем i-й столбец умноженный на ci (для всех i от 1 до m). Получим: 
Учитывая (2) получаем  Матрица T получена из матрицы B с помощью элементарных преоб-ний. Так как элементарные преоб-ния не меняют ранг матрицы, то ранг матрицы В равен рангу матрицы T.Очевидно, что ранг матрицы T =rang(A)Þ rang(A) =rang(B)
Матрица T получена из матрицы B с помощью элементарных преоб-ний. Так как элементарные преоб-ния не меняют ранг матрицы, то ранг матрицы В равен рангу матрицы T.Очевидно, что ранг матрицы T =rang(A)Þ rang(A) =rang(B)
2 ДОСТАТОЧНОСТЬ. Пусть ранг матрицы си-мы равен рангу расширенной матрицы.
Докажем, что сис-ма (1) совместна. Пусть rang(A)= rang(B)=r. Тогда матрице A есть ненулевой минор r-го порядка, а все миноры r+1-го порядка равны 0. Не нарушая общности рассуждения можно считать, что ненулевой минор r-го порядка расположен в верхнем левом углу матрицы A т.е.
 В системе (1) выделим 1-ые r уравнений
В системе (1) выделим 1-ые r уравнений  (3)
(3)
Покажем, что система (1) и (3) равносильны. Так как система (3) является частью системы (1), то любое решение системы (3) всегда яв-ся решением сис-мы (1).
Пусть a1,a2,…., am – решение сис-мы (3). Тогда при подстановке в сис-му (1) чисел a1,a2,…., am вместо x1,x2,…., xm . Первые R у-ний обратятся в верные рав-ва. Покажем, что остальные
k-r у-ний системы (1)обратятся в верное рав-тво, т.е.
at1a1+ at2a2+…+ atmam=bt , " t=r+1,r+2,…,k
Выпишем расширенную матрицу сис-мы (1)
 . Преобразуем эту матрицу следующим образом. Умножим 1-й столбец на -a1, 2-й столбец на -a2 и т.д. m-й столбец на -am и прибавим все к последнему столбцу. Получим матрицу T¢
. Преобразуем эту матрицу следующим образом. Умножим 1-й столбец на -a1, 2-й столбец на -a2 и т.д. m-й столбец на -am и прибавим все к последнему столбцу. Получим матрицу T¢

Т.к. a1,a2,…., am решение сис-мы(3), то верхние r эл-ов посл-его столбца матрицы T равны 0. Обозначим bt-at1a1-at2a2-…..--atmam=gt, t=r+1,r+2,…,k. Таким образом матрица T примет вид
 . Мат-ца T получена из мат-цы B с помощью элем-рных преобр-ний Þ rang(T)=rang(B)=r Þ В матрице T любой минор (r+1)- го порядка =0
. Мат-ца T получена из мат-цы B с помощью элем-рных преобр-ний Þ rang(T)=rang(B)=r Þ В матрице T любой минор (r+1)- го порядка =0
В частности равен 0 минор 
Т.к. по условию минор D¹0, то gr+1=0. Аналогично можно показать, что числа gr+2,… ,gk=0 Þ at1a1+at2a2+…..+atmam= bt, где t=r+1,r+2,…,k. Это означает, что последние k-r у-ний в сис-ме (1) обращаются в верные рав-тва. Þ любое решение сис-мы (3) яв-я решением сис-мы (1). Мы док-ли, что сист-ы (1) и (3) равносильны.
Опр. Лин-ное у-ние наз-ся однородным если свободный член в нем =0.Система линейных у-й состоящая из однородн. у-й наз-ся однородной. Эта сис-ма всегда совместна т.к. имеет решение x1= x2=….= xn=0. Это решение будем наз-ть нулевым реш-ем.
Теорема 5 Однородная сис-ма лин-ных у-ний имеет ненулевое решение тогда и только тогда когда ранг мат-цы сис-мы меньше числа неизвестных
Док-во. 1. Пусть однородная сис-ма имеет ненулевой ранг. Допустим, что rang(A)=n (числу неизвестных). Тогда система (1)Ûследующей крамеровской системе
 (2). Тогда (2) а значит и исходная система имеет единственное решение. И т.к. (2) однородная то это решение нулевое. Получили противоречие Þ rang(A)<n
(2). Тогда (2) а значит и исходная система имеет единственное решение. И т.к. (2) однородная то это решение нулевое. Получили противоречие Þ rang(A)<n
2. Пусть rang(A)<n тогда следуя алгоритму, мы заключаем, что система имеет бесконечно много решений, среди них будут и ненулевые.
Дата добавления: 2018-02-15; просмотров: 774; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
