Способы задания движения точки. Вычисления скорости и ускорения материальной точки при различных спосабах задания движения

Опр Материальной точкой будем наз-ть тело, размерами которого можно принебречь и положение можно будет определить ,как положение геометрической точки. Точка не имеет ориентации и её положение вполне определено 3-мя коор-ми. Говорят ,что свободная точка имеет 3 степени свободы.

Опр. Под твёрдым телом будем понимать систему ,взаимные расстояния между точками которой неизменны.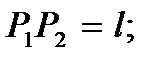

Уравнение связи 2-х точек можно представить в виде

Задать закон движения точки ,системы или тело означает установить соотношение или алгоритм ,с помощью которого их положение определены в каждый момент времени t. ЗАДАНИЕ ЗАКОНА ДВИЖЕНИЯ ТОЧКИ. Используются 3 след. способа

Векторный- для точки  мы задаём радиус-вектор  и указываем направление и расстояние. Координатный- задаёт 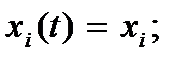 и связь орты неподвижного базиса. Естественный- задаёт закон движения траектории пути . Скоростью наз. векторную величину ,где радиус-вектор точки. Повторно дифференцируя определим ускорение.

Из курса диф. геометрии известно ,что если некая кривая Г задана в виде 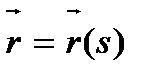,то  -единичный вектор касательной кривой Г в точке 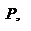определённой криволинейной абсциссой . А ,

где 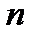-единичный вектор главной нормали кривой Г в точке  .

Он всегда расположен в соприкасающейся плоскости кривой этой точки и ориентирован к центру кривизны .Всегда направлен в сторону вогнутости .  -кривизна этой кривой,

-радиус кривизны. Единичный вектор наз. вектором бинормали.

Таким образом в каждой регулярной точки  кривой Г вводится правый трёхгранник

При естественном способе задании можно установить , что

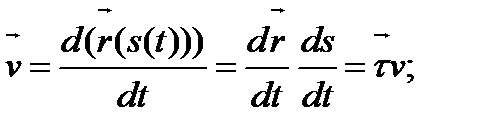
Скорость всегда касательна к траектории . Учитывая, что 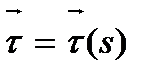,а

повторно диф-уя находим ускорение

Ускорение имеет 2 составляющие первое слагаемое наз. касательным ускорением

второе - нормальным ускорением

Причём скалярный множитель всегда положителен. Нормальное ускорение всегда ориентировано к центку кривизны.

Найти области сходимости функционального

Ряда и его сумму и исследовать её на непрерывность

Найдём сумму ряда по определению:

Т.к.  - бесконечно малая, а  -

бесконечно малая при , то ряд

сходится при .

Исследуем  на непрерывность.

1)  определена на R

2)

=>S(x) – непрерывна на R.

Условия для непрерывности:

1)  - непрер.

2)  равномерно сходится.

 

26Найти , если .

 

 

Билет 27

Поле комплексных чисел (о-ции над ком-ными числами в алг-ческой и триг-ской ф-мах; ф-ла Муавра; извлечение кв-ного корня из к-ного числа в алг-ской форме; изв-ние корня n-ой степени из комплексного числа в тригонометрической форме).

Рас-м мн-во упоряд пар (a,b) a,bÎR и обозн его через С={(a,b) ½a,bÎR}. Две пары (a,b) и(a₁,b₁) будем считать равными если a= a₁ ,b=b₁. Введем операцию сложения на С следующим образом:(a,b)+(с,d)=(a+c,b+d) (*)

Лемма 1 Алгебраическая система С с операцией сложения является абелевой группой.Док-во.1 Т.к. a+c,b+dÎR, то (a+c,b+d)ÎС следовательно операция (*) определена на С

2 ассоциативность (a,b)+((с,d)+ (e,f))= (a,b)+(с+e,d+f)= (a+(с+e),b+(d+f))= ((a+с)+e,(b+ d)+f)= (a+c,b+d)+(e,f)= ((a,b)+(c,d))+(e,f) 3 (0,0) яиляется нулевым

4 " (a,b) ÎС $ элемент (-a,-b)ÎС, являющийся противоположным

5 коммутативность

(a,b)+(с,d)=(a+c,b+d)=(с+a,d+b)=(с,d)+(a,b)

Введем на множестве С операцию умножения(a,b)*(с,d)=(aс-bd,ad+bc) (**)

Лемма 2Мн-во С^#=С\{(0,0)} с операцией (**) яв-ся абелевой группой

1 Т.к. a+c,b+dÎR, то (aс-bd,ad+bc)ÎС^#

след-но операция (*) определена на С^# 2 ассоциативность

3 (1,0) я-ся нулевым

4 " (a,b) ÎС $ элемент ÎС^#, яв-йся противоположным

5 коммутативность (a,b)*(с,d)= (aс-bd,ad+bc) (с,d)*(a,b)=(ca-db,da+cb) (a,b)*(с,d)= (с,d)*(a,b)

Теорема 1 Множество С с операциями (*) и (**) яв-я полем Док-во

1 По Лемме 1алгебраическая система (С,+) абелева группа

2 По Лемме 2 (С^#,*) абелева группа

3 " (a,b), (с,d), (e,f)ÎС

(a,b)*( (с,d)+(e,f))= (a,b)*(с+e,d+f)=(a*(c+e)-b*(d+f),a*(d+f)+b*(c+e))=( ac+ae-bd-bf,ad+af+bc+be)=(ca-bd,ad+bc)+(ae-bf,af+be)=(a,b)(c,d)+(a,b)(e,f)

Построенное поле наз-ся полем комплексных чисел, а элементы этого поля комплексными числами.

Комплексные числа в алгебраической форме

Поры вида (a,0)ÎС складываются и умножаются как действительные числа

(a,0)+(b,0)=(a+b,0)

(a,0)*(b,0)=(ab-0*0,a*0+b*0)=(ab,0)

Пару (0,1) обозначим через i. Заметим, что (b,0)*(0,1)=(b*0-0*1,b*1+0*0)= =(0,b)  След-но bi=(0,b)

Тогда компл-е число (a,b)=(a,0)+(0,b)=a+bi

Отметим, что i² = (0,1)*(0,1)=(0*0-1*1,0*1+0*1)=(-1,0)= -1

Опр Запись a+bi наз-ся алгеб-ской формой комп-го числа (a,b), число a – действительная часть, bi – мнимая часть. Из (*) и (**) следует, что (a+bi)+(с+di)=(a+c)+(b+d)*i

(a+bi)*(с+di)=(ac-bd)+(ad+bc)*i

Опр Для комплексного числа a+bi число a-bi называется сопряженным.Если a+bi=z ,то a-bi= , z= ÛzÎR/

Лемма 3 Сумма и произведение двух сопряженных чисел являютсядействительными числами.

Правило деления комплексных чисел. При делении комплексного числа на a+bi на ненулевое комплексное число c+di необходимо числитель и знаменатель дроби умножить на число сопряженное знаменателю.

Правило извлечения квадратного корня

Тригон-ская форма комп-ных чисел. Введем на пл-ти прямоугю сис коор и каждому комп чи z поставим в соот точку с коор (a,b). Это соотв будет взаимно однозначным. Действит-м точкам соотв то на оси OX. А числам вида bi соотв-ют точки на оси OY. Положение точки (a,b) полностью определяется полярными координатами.a=rcos(j) z=a+bi=rcos(j)+irsin(j) b=rsin(j)  

Запись комп-го числа в таком виде наз-ся тригон-ской формой комп-го числа.

Неотриц число r наз-ся модулем комплексного числа (½z½= ) j - наз-ся аргументом комп-го числа и обозн-ся arg zФормула для вычисления аргумента, если a=0, то    или   Arg z = если a¹0, то 1) zÎ1 или 4 четверти arctg  . 2) zÎ2 или 3 четверти arctg +p

Умножение и деление комплексных чисел в тригонометрической форме

Теорема При умножении комплексных чисел в тригон-кой форме их модули перемножаются а аргументы складываются. Док-во.Пусть z₁ =½ z₁½(cos j₁+i sin j₁) , z₂ =½ z₂½(cos j₂+i sin j₂), z₁ *z₂=½ z₁½(cos j₁+i sin j₁) *½ z₂½(cos j₂+i sin j₂)= ½ z₁½*½ z₂½( cos j_1* cos j₂+i sin j₁ cos j₂ +i sin j₂ cos j₁+i² sin j₁ sin j₂)= ½ z₁½*½ z₂½*( cos (j₁+j₂)+i sin(j₁+j₂)).

При делении комп-сных чисел их модули делятся а аргументы вычитаются.Док-во:z₃=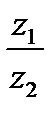Þ z₁= z₃ *z₂. По пред теореме ½ z₁½=½ z₃½*½ z₂½Þ .Argz₃= Argz₁ -Argz₂

Возведение в степень комплексного числа.При возведении в степень комп-го числа z=½ z½(cos j+i sin j), с целым показателем n его модуль возводится в степень, а аргумент умн-тся на показатель n.Т.е. zⁿ=½z½ⁿ(cosnj+isinnj)

(Для док-ва рассмотреть произведение 2 чисел(т.е. квадрата числа), затем предположить что утверждение верно для n-1 степени числа и наконец найти n-ю степень числа используя известную n-1-ю степень).  

Опр Формула zⁿ=½ z½ⁿ(cos nj+i sin nj) называется формулой Муавра

Извлечение корня из комп-го числа

Пусть nÎN n>1. Корнем n-й степени из комп-го числа z наз-ся комп-ное число c такое что cⁿ=z.

Теорема Пусть z комп-ное число, n>1 nÎN. В поле компл-ных чисел  при z=0 имеет единственное значение, а именно 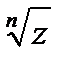=0. Если z¹0, то корень n-й степени из z имеет n различных знач-й и если z= ½ z½(cos j+i sin j), то  k=0,1,2,…

Док-во:При z=0 утв-ние очевидно.Пусть теперь z ¹0, z=½z½(cos j+i sin j). Т.к. ½z½неотрицательное число, то сущ-ет . След-но можно рассматривать ком-ное числоС_k= k=0,1,2,… Каждое из чисел С_k яв-ся корнем n-й степени из числа z. ½z½(cos j+i sin j)

Корни из единицы 1=cos 0 +i sin 0. Из предыдущей теоремы получаем

Теорема.В поле комплексных чисел имеется n различных значений , которые вычисляются по следующим формулам:  ,k=0,1,2,…

 

27Основные теоремы динамики точки: т-ма об изменении кол-ва движения, т-ма об изменении кинет-кого момента

Теорема об изменении количества движения точки.

Теорема. Производная по времени от количества движения точки равна действующей на точку силе.

Запишем основной закон динамики в виде . Так как масса постоянна, то внесем ее под знак производной.

Тогда                ,                                                                                 (*)

что и требовалось доказать.

В проекциях на координатные оси уравнение (*) можно представить в виде:

               

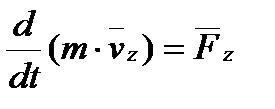
Теорема об изменении момента количества движения точки.

Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.

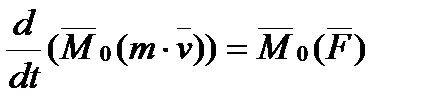
Доказательство: Продифференцируем момент количества движения по времени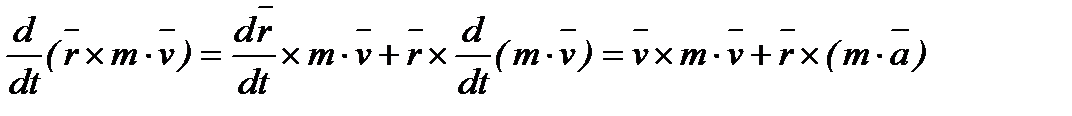

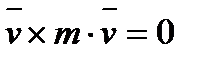,    ,следовательно ,                 (*)

что и требовалось доказать.

Теорема. Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси.

Для доказательства достаточно спроектировать векторное уравнение (*) на эту ось. Для оси это будет выглядеть так:               

Следствия из теорем:

1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.

,             

2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.

,          

---

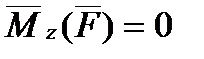Дата добавления: 2018-02-15; просмотров: 599; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!