Привести к каноническому виду
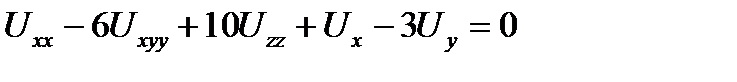
Решение

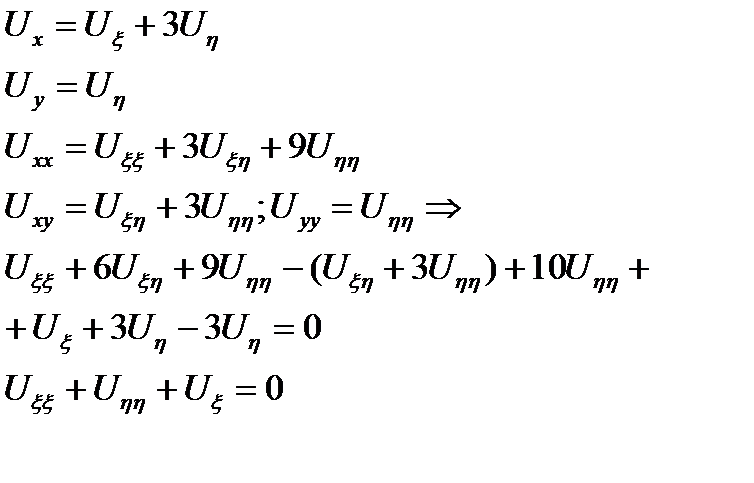
29Тело вращается вокруг неподвижной оси согласно закону 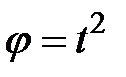 . Определить скорость точки тела на расстоянии
. Определить скорость точки тела на расстоянии 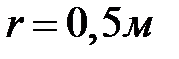 от оси вращения в момент времени, когда угол поворота
от оси вращения в момент времени, когда угол поворота 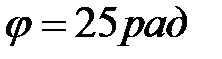 .
.
Дано:Решение:
ОА=r=0,5м 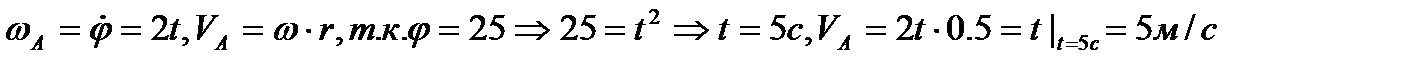
j=t2
VA-?
 Ответ:VA=5м/с
Ответ:VA=5м/с
Билет 30
Криволинейные и поверхностные интегралы. Формула Остроградского. Формула Стокса.
Т-ма (формула Стокса): Пусть Ф – это поверхность, заданная x=x(u,v), y=y(u,v), z=z(u,v), где (u,v)Îплоской области Д, ограниченной кусочно-гладким контуром L. Предполагается, что Ф – это гладкая, т.е. функции x, y, z – непрерывно дифференцируемы и отображение из Д в Ф взаимнооднозначно и взаимнонепрерывно, при этом контур L отображается в L. Ф без особых точек. На поверхности выбрана сторона  , а на контуре L положительное направление.
, а на контуре L положительное направление.
Формула Стокса в развернутом виде:
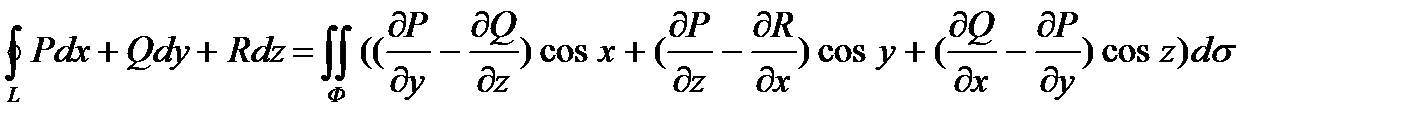 Т-ма (формула Гаусса-Остроградского)Пусть V – тело, ограниченное кусочно-гладкой поверхностью Ф (замкнутой). Пусть
Т-ма (формула Гаусса-Остроградского)Пусть V – тело, ограниченное кусочно-гладкой поверхностью Ф (замкнутой). Пусть  - векторное поле (P,Q,R), определенное и непрерывное на замыкании Vвместе со своими частными производными
- векторное поле (P,Q,R), определенное и непрерывное на замыкании Vвместе со своими частными производными 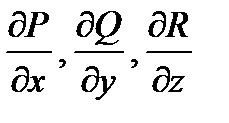 , тогда поток векторного поля через поверхность Ф равен тройному интегралу от дивергенции
, тогда поток векторного поля через поверхность Ф равен тройному интегралу от дивергенции 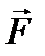 по телу, ограниченному этой поверхностью.
по телу, ограниченному этой поверхностью.
Поток векторного поля 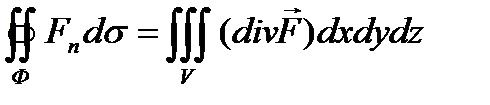 .
.
Покоординатный вид формулы Г.-О.:
 .
.
Левую часть можно записать в виде поверхностного интеграла 2-го рода:
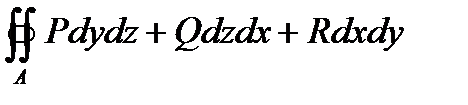 .
.
Кольцо мног-нов от одной переменной (теорема о делении с остатком, алгоритм Евклида и нахождение наибольшего общего делителя двух мног-нов с его помощью; корни мног-ов; т-ма Безу; осн-ная т-ма алгебры комп-ных чисел (т-ма Гаусса) и её следствия; комп-ные корни мног-нов с действительными коэф-тами).
|
|
|
Пусть А некоторое кольцо с единицей, построим новое кольцо В элементами которого будут является упорядоченная последовательность, элементы которого принадлежат А.
Т-ма: (О кольцах многочленов)Множество В с операцией * (сложения) и ** (умножения) образует кольцо с единицей.
Т-ма: (о делении с остатком)Пусть Р- поле и g(x) ненулевой многочлен из кольца Р[х], тогда каждому многочлену f(x) 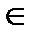 Р[х] cоответствует единственная пара многочленов q(x),r(x)
Р[х] cоответствует единственная пара многочленов q(x),r(x) 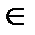 Р[х] такая что f(x)=q(x)g(x)+r(x), причем degr(x)<degg(x), где q – неполное частное, r – остатком.
Р[х] такая что f(x)=q(x)g(x)+r(x), причем degr(x)<degg(x), где q – неполное частное, r – остатком.
О: Если многочлены f(x) и g(x) делятся на многочлен d(x), то многочлен d(x)- называется их общим делителем. Если многочлен d(x)- яв-ся общим делителем f(x) и g(x) и делится на другой делитель этих многочленов, то он называется НОД этих многочленов. НОД(f(x),g(x))=d(x)
Алгоритм Евклида и его приложения.
Пусть f(x) и g(x) 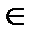 Р[х], где Р- поле. Пусть многочлен g(x) – ненулевой. Если g(x)|f(x)? То НОД(f(x),g(x))=g(x).
Р[х], где Р- поле. Пусть многочлен g(x) – ненулевой. Если g(x)|f(x)? То НОД(f(x),g(x))=g(x).
Пусть g(x) не делит f(x), то по теореме о делении с остатком f(x)=g(x)q 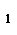 (x)+r
(x)+r 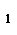 (x), deg r
(x), deg r 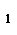 (x)<degg(x),
(x)<degg(x),
|
|
|
g(x)= r 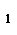 (x)q
(x)q 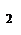 (x)+r
(x)+r 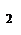 (x), deg r
(x), deg r 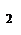 (x)<deg r
(x)<deg r 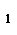 (x) ,
(x) ,
r 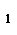 (x)= r
(x)= r 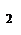 (x) q
(x) q 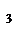 (x)+ r
(x)+ r 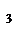 (x), deg r
(x), deg r 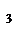 (x)<deg r
(x)<deg r 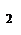 (x),
(x),
…………………………………………………..
r 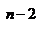 (x)= r
(x)= r 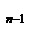 (x) q
(x) q  (x)+ r
(x)+ r  (x), deg r
(x), deg r  (x)<deg r
(x)<deg r 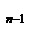 (x) (1)
(x) (1)
r 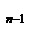 (x)= r
(x)= r  (x) q
(x) q  (x)
(x)
deg g(x)> deg r 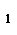 (x)>….> deg r
(x)>….> deg r  (x)
(x)
Цепочка равенств (1) называется алгоритмом Евклида.
Т-ма: Если f(x) и g(x) 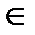 Р[х], где Р- поле и g(x) – ненулевой, то НОД этих двух многочленов всегда существует. Если g(x)|f(x) то НОД(f(x),g(x))=g(x), если же g(x) не | f(x), то НОД(f(x),g(x))=
Р[х], где Р- поле и g(x) – ненулевой, то НОД этих двух многочленов всегда существует. Если g(x)|f(x) то НОД(f(x),g(x))=g(x), если же g(x) не | f(x), то НОД(f(x),g(x))=
последнему ненулевому остатку в алгоритме Евклида.
О: Если многочлен f(x) над полем Р степень которого  1, не имеет других делителей, кроме многочленов а и а f(x), где а
1, не имеет других делителей, кроме многочленов а и а f(x), где а 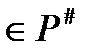 , то f(x) – называется неприводимым многочленом над полем Р.
, то f(x) – называется неприводимым многочленом над полем Р.
Т-ма: всякий многочлен f(x ) степень которого 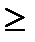 1 над полем Р – можно представить в виде произведения неприводимых над полем Р многочленов.
1 над полем Р – можно представить в виде произведения неприводимых над полем Р многочленов.
Пусть Р- поле, f(x) = anxn+ an-1xn-1+…+ a0 ÎP[x], cÎP. Тогда f(с) = anсn+ an-1сn-1+…+ a0 называют значением многочлена f(x) для с.
Если f(с) = 0, то с – корень f(x).
Т-ма (Безу):cÎP является корнем f(x) ÎP[x] Ûf(x) = (х – с)q(x), q(x) ÎP[x].
Док-во:f(x) = (х – с)q(x) + r(x), degr(x) <deg(x – c)=1, т.к degr(x) может быть либо 0,
либо -¥, то r(x) = rÎP. f(с) = (с – с)q(x) + r(x) = 0q(x) + r = r.Следовательно f(х) = (х – с)q(x) + f(с) (#)
|
|
|
1) Если cÎP является корнем f(x), то f(с) = 0 Þ из (#)f(х) = (х – с)q(x).
2) Если f(х) = (х – с)q(x), то f(с) = (с – с)q(с) = 0 Þc является корнем f(x).
Т-ма (Гаусса):В поле C многочлен из C[x] имеет хотя бы один корень, если deg многочлена ³1.
Следствие 1:В поле комплексных чисел f(x) Î С[x] имеет ровноn корней, если degf(x) = n³1.
Следствие 2:Неприводимыми над С являются только многочлены 1-ой степени.
Т-ма (корни многочленов с действительными коэффициентами):
Док-во:Пусть f(x) = anxn+ an-1xn-1+…+ a1х + a0, т.к. z – корень, то f(z) = 0, т.е.
an z n+ an-1 z n-1+…+ a1 z + a0 = 0.
Пусть f(x)ÎR[x], z = a + b×i – корень f(x), тогда 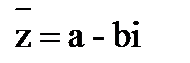 тоже корень f(x).
тоже корень f(x).

Следствие 1:Многочлен над R нечетной степени имеет хотя бы 1действительный корень.
Следствие 2:Неприводимыми над R являются многочлены первой степени и второй степени с отрицательным дискриминантом.
30Исследовать характер изолированных особых точек ф-ции 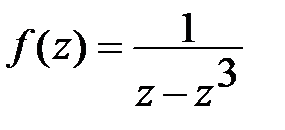 , включая и точку
, включая и точку 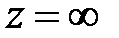 . Найти вычеты ф-ции f в этих точках.
. Найти вычеты ф-ции f в этих точках.
Решение:z1=0, z2=1, z3=-1, z4=¥. Используем критерий полюса для исследования 1-х трех изолированных особых точек: Точка z явл-ся полюсом m-го порядка f(z) Û для ф-ции  – z0 явл-ся нулем m-го порядка.
– z0 явл-ся нулем m-го порядка.  =z(1-z)(1+z)=z-j(z) j(0)¹0 и j(z) явл-ся аналитической в окрестности точки 0. След-но z1=0 явл-ся нулем 1-го порядка для ф-ции
=z(1-z)(1+z)=z-j(z) j(0)¹0 и j(z) явл-ся аналитической в окрестности точки 0. След-но z1=0 явл-ся нулем 1-го порядка для ф-ции  Þz1 – полюс 1-го порядка для f(z).
Þz1 – полюс 1-го порядка для f(z).
|
|
|
Аналогично z2 и z3 явл-ся полюсами 1-го порядка.
Найдем вычеты в этих точках.
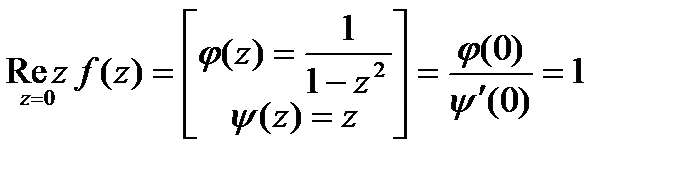 ;
; 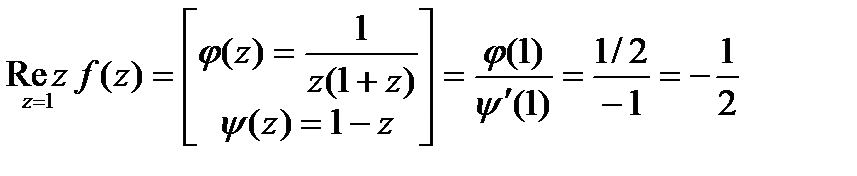
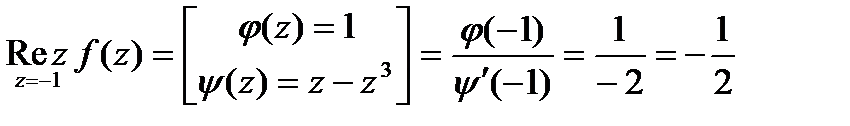 . В силу т-мы: сумма вычетов во всех изолированных особых точках включая ¥ =0. След-но
. В силу т-мы: сумма вычетов во всех изолированных особых точках включая ¥ =0. След-но 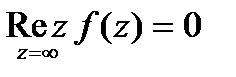 .
.
Осталось классифицировать особую изолированную точку z=¥. 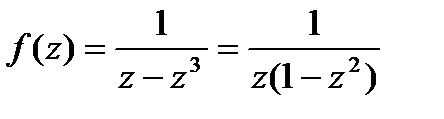 .
.
Разложим по степеням z: 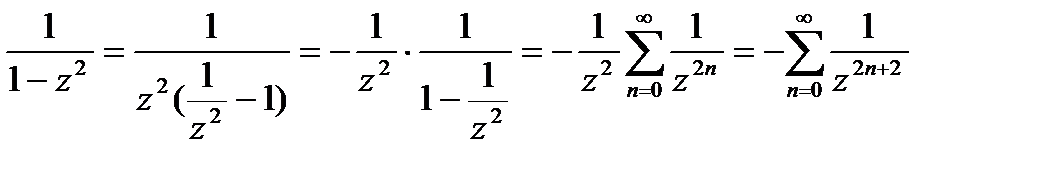 . Т.о.
. Т.о.  т.к. в ряде Лорана отсутствует главная часть, то точка z=¥ явл-ся устранимой особой точкой.
т.к. в ряде Лорана отсутствует главная часть, то точка z=¥ явл-ся устранимой особой точкой.
30. Дифференциальное уравнение колебательного движения материальной точки имеет вид  . Определить период затухающих колебаний.
. Определить период затухающих колебаний.
Решение:
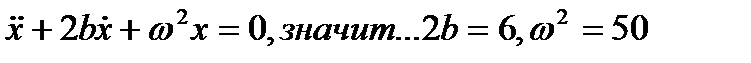
Частота: 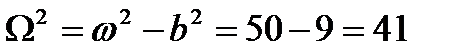 ; период:
; период: 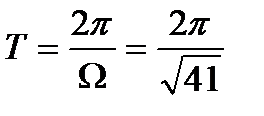
Ответ: 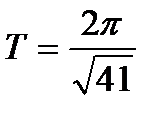 .
.
Дата добавления: 2018-02-15; просмотров: 619; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
