Найти решение указанной задачи

 

 

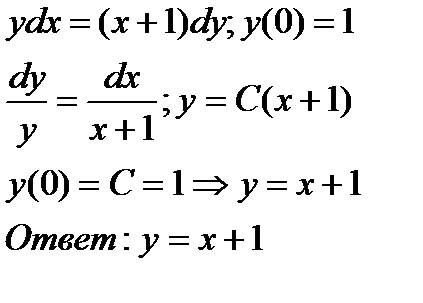
Билет 25

25Выборка и генеральная совокупность. Несмещенность, эффективность и состоятельность оценок. Критерий согласия .

Предположим, что в одинаковых условиях и независимо друг от друга производиться n измерений случайной величины -конкретная выборка объёма n из распределения F(x), где F(x)-функция распределения случайной величины x. Если смотреть на результаты измерения до того как они будут проведены,

то это будут случайные величины , имеющие ф-цию распределения F(x). Они независимы.

Говорят, что случайные величины  образуют абстрактную выборку объёма n из распределения F(x), если они независимы и каждая из них имеет ф-цию распределения F(x). Бесконечная совокупность случайных величин с одной и той же ф-цией распределения F(x) наз-ся генеральной совокупностью.

Пусть есть выборка x1,x2,…,xn из распределения F(x) зависящая от неизвестного параметра a.

Оценкой или статистикой неизвестного параметра a наз-ся любая борелевская ф-ция 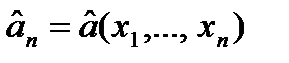от значений выборки.

Оценка  неизвестного параметра a наз-я несмещённой, если

Оценка  неи-ного пар-ра a наз-ся состоятельной, если  и сильно состоятельной, если

Оценка  неизв-го па-тра a наз-ся эффективной, если среди всех возможных оценок параметра a она минимизирует , т.е. это оценка с наименьшей дисперсией.

Критерий.Пусть x1,x2,…,xn-выборка, причём F(x) неизвестна. Пусть 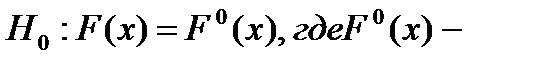заданная ф-ция распределения. Гипотезы такого вида наз-ся гипотезами согласия, а критерии для них= критериями согласия.

Т-ма Пирсона При , где  с (к-1) степенями свободы. относительная частота того, что { } не очень большая.

Пусть

Вид критической области K={ } (если пары пересекаются, то гипотеза отвергается)

Задаём уровень значимости .

}=

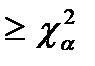(100 %; k-1)

если , то гипотеза H0 отвергается.

-гипотеза не противоречит экспериментальным данным.

 

 

Кривые второго порядка (упрощение общего уравнения линии второго порядка с помощью преобразования системы координат; канонические уравнения кривых второго порядка).

Опр. Кривой второго порядка наз мн-во точек пл-ти, коорд-ты которы векоторой прямоугольной системе коорд-т удовл ур: ax²+bxy+cy²+dx+ey+f=0(1)

где a ,b ,c одновременно ¹0.Слогаемые, содержащие квадраты координат и их произведение наз. старшими членами ур (1).

С помощью преобразования системы коотд-т общее ур кривой второго порядка может быть преобразовано к одному из видов:

1. действительный эллипс

2. мнимый эллипс

3. гипербола

4. пара действительных, пересекающихся прямых a²x² - b²y²=0

5. пара мнимых прямых, пересекающихся в действительной точке a²x² + b²y²=0

6. парабола

7. пара действительных параллельных прямых y²=a²

8. пара мнимых параллельных прямых y²= - a²

9. пара действительных совпадающих прямых y²=0

Примером кривых второго порядка является окружность (x-a)²+(y-b)²=R², где (a, b)- центр окружности.

Эллипсом наз множ-во точек пл-ти, для кажд из кот сумма расстояния для двух данных точек называемых фокусами, есть величина постоянная и большая чем расстояние между фокусами.

Гиперболой наз множ-во точек пл-ти, для кажд из кот разность расстояние до двух данных точек, называемых фокусами есть величина постоянная и меньшая чем расстояние между фокусами.

Параболой наз множ-во точек пл-ти, для кажд из кот разность расстояние до точки, называемой фокусом равно расстоянию до прямой , называемой дириктрисой.

y²=2px.

---

Дата добавления: 2018-02-15; просмотров: 581; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!