Аксиомы теории вероятностей. Классическое определение вероятности. Схема Бернулли.
Пусть  -пространство элементарных исходов (множество единственно возможных неразложимых исходов случайного эксперимента).
-пространство элементарных исходов (множество единственно возможных неразложимых исходов случайного эксперимента).
Пусть F- некоторая  -алгебра подмножеств пространства
-алгебра подмножеств пространства  , т.е.
, т.е.
1) F- алгебра: а)  ÎF,ÆÎF
ÎF,ÆÎF
б) если A,BÎF, то A  BÎ F, A\BÎ F, ABÎ F
BÎ F, A\BÎ F, ABÎ F
2) 
Событием называется произвольное подмножество A пространства W, входящее в  -алгебру F.
-алгебру F.
Любому событию A, ставится в соответствие действительное число P(A), называемое вероятностью события A так, что при этом выполняются следующие 3 аксиомы:
1) Аксиома неотрицательности
P(A)³0 "AÎF
2) аксиома нормированности
P(W)=1
3) аксиома счётной аддитивности
 "
"  , где
, где
An несовместимы попарно, т.е. AiÇAi-1=Æ
(W,F,P), где W-пространство элементарных исходов, F-некотарая фиксированная  -алгебра подмножеств W, P- вероятность, определённая на
-алгебра подмножеств W, P- вероятность, определённая на  -алгебре F называется вероятностным пространством.
-алгебре F называется вероятностным пространством.
Рассмотрим частный случай. Предположим что W-дискретное пространство элементарных исходов. F={A½AÌW}, {w}ÌF, P({w})-вероятность этого события (элементарный исход-ЭИ).
1) Вероятность ЭИ P({w})=p(w)³0 "wÎW
2) Всё пространство W можно представить в виде суммы конечного или счётного одноточечных множеств из W, т.е.
W=  1
1  т.е.
т.е.  =1
=1
AÌW; A=  В силу свойства III
В силу свойства III 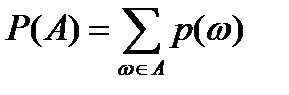 Þ
Þ
Чтобы получить вероятность события A необходимо подсчитать вероятность элементарных исходов, благоприятствующих этому событию.
Классическое определение.
Если пространство элементарных исходов конечно, а все исходы равновероятны, то вероятностью события A называется отношение числа исходов благоприятствующих A к числу всех возможных исходов.
|
|
|
Схема Бернулли.
Формула Бернулли имеет вид  , где p-вероятность удачи, q- вероятность неудачи.
, где p-вероятность удачи, q- вероятность неудачи.
Различные виды ур-ний прямой на пл-ти (общее; по двум точкам; по угловому коэффициенту и точке; каноническое; параметрические; в отрезках по осям).
Ур прямой с угл коэф-том.
Опр. Угл коэф-т прямой на пл-ти наз тангенс угла, кот образует эта прямая с положительным направл-ем оси ОХ. т.е. если к -угл коэф-нт, то по опр. tga=к.
Пусть положение прямой в пл-ти (ХУ) определяется её угл.коэф. и отрезком ОВ, кот. Она отсекает по оси ОУ. Пусть М(х,у)- любая т. этой прямой.
a) y=kx+b (1)—ур прямой с угл коэф-м.
Частные случаи:
1. к¹0, b=0, y=kx –ур прямой , проходящей ч/з начало координат.
2. к=0,b¹0, y=b – ур прямой  оси ОХ.
оси ОХ.
3. к=b=0 у=0 –это ур оси ОХ.
b) Ур прямой по угл коэф и точке.y-y1=k(x-x1)
c) Ур прямой по 2 точкам. 
d) Ур прямой в отрезках по осям. 
e) Параметрическое ур прямой.
Опр. Направляющим вектором пряой явл "ненулевой вектор, кот коллинеарен данной прямой.
 a(a1, a2)-направляющий вектор, M0M=
a(a1, a2)-направляющий вектор, M0M=  t, t – некоторое число.
t, t – некоторое число.
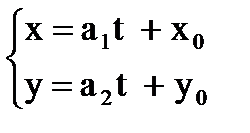
f) Общее ур прямой.
|
|
|
Теорема.Всякому ур вида Ax+By+C=0 (6), где А2+В2¹0 в пл-ти (Х, У) соответствует некотор прямая (А2+В2¹0 означает, что коэф-ты А и В одновремено ¹0).
Док-во: пусть дано ур 6, где А2+В2¹0. Допустим, что В=0, тогда А¹0 и ур принимает вид Ах+С=0, Þ 
 Этому ур удовлетворяет множ-во точек, каждая из которых имеет одну и ту же абсциссу. т.е. все это точки будут расположены на прямой
Этому ур удовлетворяет множ-во точек, каждая из которых имеет одну и ту же абсциссу. т.е. все это точки будут расположены на прямой  оси ординат.
оси ординат.
Пусть В¹0, тогда из ур (6) имеем  ,
,  ,
,  Þy=kx+b, но это есть ур прямой с угл коэф-м. ч.т.д.
Þy=kx+b, но это есть ур прямой с угл коэф-м. ч.т.д.
Теорема(обратная , об общем уравнении прямой). Всякой прямой в пл-ти (Х, У) соответствует лин ур вида Ax+By+C=0 (6), где А2+В2¹0.
23Решить задачу Коши:

Решение
Это волновое уравнение

23Улучшить план  задачи на безусловный минимум
задачи на безусловный минимум
 методом наискорейшего спуска (одна итерация).
методом наискорейшего спуска (одна итерация).
Решение:
Находим градиент 

Направление итерации 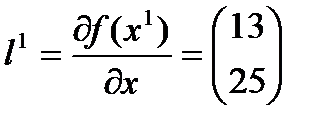 в
в 
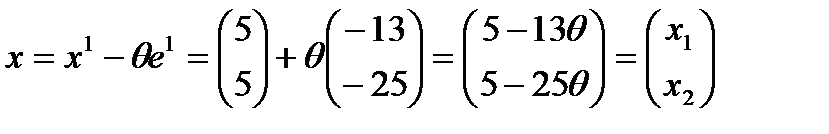
Этот вектор х поставим в функцию:

 Þ шаг q0
Þ шаг q0 

Проверка: f(x1)=90, f(x2)=11383,03, Df(x)= 11383,03-90=11293,03 условная функция должна увеличиваться.
Ответ: 
Билет 24
Дата добавления: 2018-02-15; просмотров: 592; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
