Изменить порядок интегрирования в

Следующих повторных интегралах

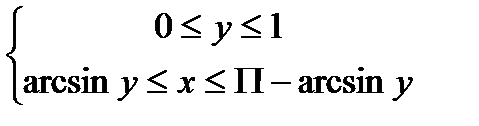
I = .

20Через прямую x = 2 + 5t, y = 3 + t, z =

–1 + 2t проведите плоскость, перпендикулярную к плоскости 4x + 3y – z + 3 = 0.

Решение:

Направляющий вектор прямой (коэффициенты при параметрах)

Нормальный вектор плоскости , координаты точки А=(2,3,-1).

- нормальный вектор построенной плоскости. Если плоскость проходит ч\з прямую, то нормальный вектор плоскости перпендикулярен направляющему вектору прямой, т.е. и кроме того

Т.о. , где В – произвольное число, пусть В=13, тогда и уравнение плоскости имеет вид: -7x+13y+11z+D=0. Подставив в это уравнение координаты точки А, найдем D=-14, т.о. -7x+13y+11z-14=0.

Ответ: -7x+13y+11z-14=0.

Билет 21

Интегральная теорема Коши. Разложение аналитической функции в ряд Тейлора. Интегральная формула Коши.

Т(Инт т Коши) Если G-односв обл в C и f –однозн анал в эт обл ф-я, то для люб замкн спрямляемой кривой L, леж в G, интегр от f вдоль L равен нулю: .

Здесь означ интегр по замкн конт L с обходом «против час стрел». Аналог утв-е (обобщ интегр теор Коши) им место и в том сл-е, когда G-внутрен-ть жордан-й спрямляемой кривой L, а f-ф-я, непрер в и аналит в G. Из этой теор след, что интегр от ф-и f , аналит-ой в односв обл G, завис только от нач и кон-й точек пути интегрир-я. Поэт для интегр вдоль спрямл-й кривой L, леж в обл G и соед точки z и z₀, польз обознач , zz0-пред интегрир.

Инт ф-ла Коши: Пусть f(z)-однозн и анал в обл G ф-я, а L-замкнут жорд спрямляемая кривая, принадлеж G вместе со своей внутренностью D. Тогда для произв-й т. справ ф-ла: .

Инт-л, стоящ в прав части назыв инт-м Коши, след: 1)кажд анал ф-я в обл G бескон.число раз диф-ма в ней; 2) произ анал ф-ии в обл G сама явл ф-ей анал-ой в G; 3) действит и мним части анал ф-ии в G облад диф-ми част произв-ми всех пор-ов; 4) если L-замкнут жорд спрямл кривая, принадл G вместе со своей внутренностью D, а f(z)-анал в G, то для произвольной т. и люб натур k справ рав-во: .

Теор: Если ф-я f анал-я, то в окр произ т. , ф-я , причём R ряда не меньше, чем 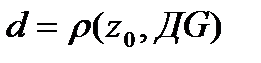, а коэф , где =окр с центр в т. , .

Принцип Лагранжа снятия ограничений (для задач с ограничениями в виде равенств).

Принцип Лагранжа снятия ограничений для задач с ограниченными равенствами.

По параметрам задачи c'x→max, Ax=b, x≥0, вводим функцию Лагранжа.

F(x,λ)= λf(x)+ Σλ_ig_i(x)= λ₀f(x)- x₀λ(x) - обобщенная функция Лагранжа.

F(x,λ)= f(x)+ λ'g(x).

λ= λ_i_-множители Лагранжа.

λ - обобщенный λ - классический вектор Лагранжа.

F(x,λ)_λ₀₌₁ = F(x,λ).

Обобщенное правило Лагранжа: если Х⁰ - ЛОП, тогда существует такой обобщенный вектор Лагранжа λ⁰, λ⁰≠0. .

Из числа задач 1 можно выделить такой подкласс, который с одной стороны является достаточно широким, ему принадлежат практически все задачи возникающие в приложениях, а с другой стороны, для которых правило Лагранжа справедливо в классической форме (λ⁰₀=1).

Обобщенное и классическое правило Лагранжа вместе образуют т.н. принцип Лагранжа снятия ограничений, согласно которого ОП и ЛОП задачи (1) следует искать среди решений системы и системы .

21Даны два базиса и пространства Найти матрицу перехода от базиса к .

Решение:

Так как векторы е₁, е₂ образуют базис пространства, то векторы а₁ и а₂ можно линейно выразить через е₁, е₂:

а₁=α₁₁е₁+α₁₂е₂ или (-2, -4)=α₁₁(1, -2)+ α₁₂(3, 2)

а₂=α₂₁е₁+α₂₂е₂(-1, -6)= α₂₁(1, -2)+ α₂₂(3, 2)

Каждое из этих равенств можно заменить системой уравнений 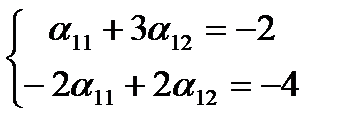α₁₁=1, α₁₂= -1. α₂₁=2, α₂₂= -1

Тогда матрица перехода:

Ответ:

21 21К акая плоская фигура задана уравнением: x² – 4y² + 4x + 24y – 36 = 0.

Решение:

Выделяем полные квадраты: (x²+4x+4)-4(y²-6y+9)-36-4+36=0; (x+2)² – 4(y-3)² – 4=0;

(x+2)² – 4(y-3)² = 4; /:4 -- получили уравнение гиперболы.

-2 -1 2

Дата добавления: 2018-02-15; просмотров: 558; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 18 19 20 21 222324 25 26 27 Следующая ⇒

Мы поможем в написании ваших работ!