Аксиома: пусть а произв прамая, А точка не лежащая на ней, тогда в плоскости определенной а и точкой А можно провести по крайней мере 2 прямые не пересек. прям. а.
модельКэли-клейна:
используя понятие Евкл. геом построили модель геометрии Лобачевского.
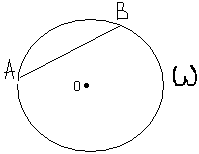
Рассм окресность единичного радиуса с центром в точке О. Эту окружность назовем w-абсол.,
Ω-круг, огранич. окресностью w. E= Ω= Ω\w-мн-во внутренних точек окресности.
F={мн-во хорд с концами на w}- прямые
Отношения принадлежности и порядка определяются косвенным образом, как и в Евклид. геом.
Отношения р-ва определяются спец. образом с помощью λ-преобразования. Далее проверяется выполнимость в данной геометрии всех аксиом геометрии
17Разложить функцию f(z) = 
в ряд Лорана в кольцах 
и 
Решение:
1) Разложим по степеням z -1
; 
; 
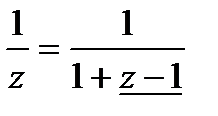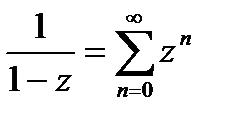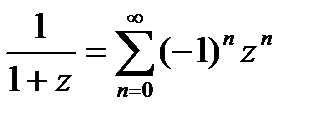
Тогда 
; f(x)= 
2) Разложим по степеням z
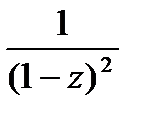сначала разложим 
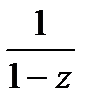это геометр прогрессия 
В круге сх-сти степенной ряд можно почленно дифференцировать " количество
раз. Дифференцируем 
.
Найти решение указанной ниже задачи
Билет 18
Лнейные функционалы и операторы(норма оператора; связь непрерывности линейного оператора с его ограниченностью; теорема Банаха-Штейнгауза (принцип равномерной ограниченности); теорема Банаха об обратном операторе).
Отображение норма действ из вект. пр-ва Х в R будем называть нормой на Х если 1)||x||≥0 " хÎХ ||x||=0 óx=0; 2)||λx||=|λ|·||x|| " хÎХ, " λÎК; 3) ||x+y||≤||x||+||y||
Векторное пространство Х с заданной на нем нормой называется нормированным пространством." нормированное пр-во явл. метрическим пр-вом. Метрика вводится след-м образом r(х,у)=||x-y||
|
|
|
Проверим, что выполняются аксиомы метрики: 1)r(х,у)=0 Þ ||x-y||=0 Þx=y ||x-x||=0 (обратное очевидно); 2)очевидно ||x-y||=||y-x||; ||x-y||=||(-1)(y-x)||=|-1| ||y-x||= ||y-x||; 3)r(х,у) ≤r(х,z)+ r(z,у)
Полное нормированное пространство наз банаховым простр. (полное нормированное простр-во явл метрическим, то понятие полного нормированного пространства означает, что оно полное как метрич пр-во относительно метрики r(х,у)= ||x-y||
Пусть Х1 и Х2 – линейные пр-ва, над одним и тем же полем R, отображение А:Х1®Х2 будем называть линейным отображением или линейным оператором, если 1) А(х,у)=А(х)+А(у) "х,уÎХ1 ; 2) А(lх)=lА(х) "хÎХ1, "lÎК. Если Х2=К (R или С), то линейное отображение А будем называть линейным функционалом.
Линейный оператор А:Х1®Х2, Х1, Х2 нормированные пр-ва, называется ограниченным, если для "хÎХ1, ||Ах||Х2£с||х||Х1 с- некоторая константа не зависящая от х.
Линейный функционал наз ограниченным, если он ограничен как оператор т.к. функционал это частный случай линейного оператора.
Т1 Пусть А:Х1®Х2 линейный оператор действующих из нормированного пр-ва Х1 в нормированное пр-во Х2, тогда Þ е условия равносильны 1) А – непрерывен в 0; 2) А – непрерывен; 3) А- равномерно непрерывен; 4) А – ограничен.
|
|
|
ТБанаха-Штейнгаусса. Пусть Х,У – нормированные пр-ва, Х- банахово пр-во, пусть МÌL(х,у), т.е. М- мн-во линейных ограниченных операторов действущий из Х вУ, причем: "хÎХ,$ const Cx : ||Ax||£Cx"AÎM, тогда $ абсолютная const С>0 : ||A||£С "АÎМ
ТБанаха об обратном операторе. Пусть А – линейный ограниченный оператор действующий из нормированного пр-ва Е1 в Е2 взаимнооднозначно отображая Е1 на Е2, и пусть Е1 и Е2 банаховы пр-ва, тогда А-1$ и ограничен. ДОКАЗАТЕЛЬСТВО: $-е обратного оператора Þ-т из того что А взаимно однозначно отображает Е1 на Е2 линейность доказана. Остается проверить,что А-1 ограниченный оператор и поскольку условие ограниченности равносильно усл непрерывности, то воспользовавшись критерием непрерывности отображения А, а именно отображения А – непр, если прообраз открытого мн-ва явл открытым, достаточно показать, что (А-1)-1(U) явл открытым "U – откр в Е1Þ (А-1)-
1(U)=А(U) – открыто по теореме об открытом отображении. (ч.т.д.)
Дата добавления: 2018-02-15; просмотров: 450; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!