Криволинейные и поверхностные интегралы (формула Грина; условия независимости криволинейного интеграла от формы пути).

Криволинейные интегралы первого рода.

Пусть g - спрямляемая кривая (т.е. которая имеет длину), (x(s),y(s),z(s)), где s – переменная длина дуги, естественный параметр. r=r(s) , где r – трехмерный вектор и имеет координаты (x(s),y(s),z(s)). Функция r=r(s) называется представление кривой. В данном случае кривая задана с помощью натурального естественного параметра. Важно и направление на кривой. Направление обычно берется соответственно возрастанию параметра. Рассмотрим произвольное разбиение t отрезка [0,s] точками s₀=0, s₁,…,

s_i=s. В каждом из частичных отрезков отметим точку x_i, найдем соответствующую точку r(x_i) на кривой g. Отметим также точки r(s_i_-1) и r(s_i). Получим разбиение кривой с отмеченными точками. Пусть f(x,y,z) – функция, заданная на кривой g. Дополнительно предположим, что эта функция непрерывна на кривой g, не обязательное, но обычное предположение. Рассмотрим ,которая наз-ся интегр-ной суммой для крив-ного интеграла 1-го рода, соответствующей разбиению t и выбору отмеченных точек x_i.

Опр: Кривол-ный интеграл 1-го рода наз-ся предел интегральных сумм при мелкости разбиения, стремящейся к нулю (если он $, то тогда ф-цию наз-ют интегрируемой, если не существует, то – неинтегрируемой).

Криволинейные интегралы второго рода.

Дано: кривая , - гладкая, т.е. x= , y= , z= , где a£t£b, - непрерывно дифференцированы и заданы 3 ф-ции 3-х переменных:

P(x,y,z), Q(x,y,z), R(x,y,z) – заданы на кривой g и непрерывны на ней.

Опр: Криволинейный интеграл 2-го рода от отображения F(P,Q,R) наз-ся .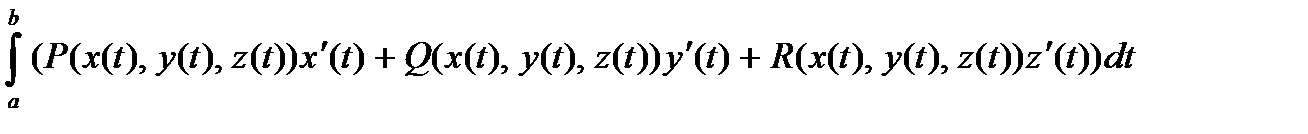

Обозначение: .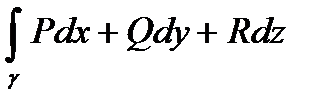

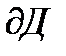Т-ма (о формуле Грина): Пусть P(x,y) и Q(x,y) – непрерывны вместе со своими частными производными в замкнутой области Д, ограниченной одним или несколькими кусочно-гладкими контурами. Тогда , где Д – наша область, - граница области, где на каждом из контуров, образующих границу, берется положительное направление и криволинейный интеграл, стоящий слева, есть сумма интегралов по этим контурам.

Т-ма ( условие независимости криволинейного интеграла от формы пути): Пусть P(x,y), Q(x,y) – непрерывны в области Д. Тогда следующие условия эквивалентны:

1. интеграл по любому замкнутому контуру, лежащему в области Д, равен нулю.

2. для любых точек А и В ÎД не зависит от выбора кривой, соединяющей точки А и В.

3. выражение Pdx+Qdy является полным дифференциалом, т.е. $ такая функция U(x,y) (она называется потенциал), такая что Pdx+Qdy= 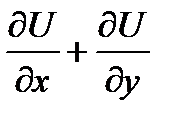, иначе говоря P= , Q= . В этом случае = U(x(b),y(b))-U(x(a),y(a)).

Поверхностный интеграл 1-го рода.

Пусть Ф – двусторонняя кусочно-гладкая повер-сть, огр-ная кусочно-гладким контуром М(x,y,z). Пусть f- ф-ция, заданная в точках повер-сти Ф.

1. Разобьем Ф на части Ф₁, …, Ф_n( ) – кусочно-гладкими кривыми.

2. В каждой части произвольным образом выберем точку М_i(x_i ,y_i ,z_i).

3. Значение функции f умножим на площадь кусочка Ф_i : f(x_i ,y_i ,z_i)S(Ф_i).

4. Рассмотрим сумму, полученную в произведении f(x_i ,y_i ,z_i)S(Ф_i) (она наз-ся интегральной).

5. Предел этих интегральных сумм при мелкости разбиения ®0 (если он $) наз-ся повер-тным инт-лом 1-го рода ф-ции f по поверхности Ф и обозначается .

Поверхностный ин-л 2-го рода.

Пусть Ф двусторонняя гладкая повер-сть, огр-ная кусочно - гладким контуром. Выберем сторону повер-ти (т. е. выбрать вектор или - ).

Пусть f(x,y,z) – ф-ция, заданная в точках этой повер-ти Ф. Рассмотрим разбиение пове-сти Ф. В каждом Ф_i выберем произвольную точку М_i( ) , значение ф-ции в этой точке f(М_i) умножим на cos S(Ф_i), т.е. f(М_i)cos S(Ф_i), где cos - косинус угла, образованного выбранным вектором нормали в точке М_i и полож-ным направлением оси OZ. Рассмотрим сумму , она наз-ся интег-ной суммой для повер-стного инт-ла 2-го рода. Если предел интегральных сумм при мелкости разбиения стремится к 0, $ , то ф-ция наз-ся интегрируемой, а этот предел инт-лом 2-го рода, который обоз-ся 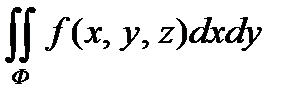. Аналогично определяются инт-лы: и .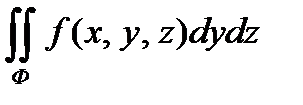

Итак, =

= .

13. Б 13 Используя первую интерполяционную формулу Ньютона для равноотстоящих узлов вычислить приближенное вычисление значение функции в точке x = 1,25.

x	y
1.2	2,0736
,3	2,8561
1,4	3,8416
1,5	5,0625

i	xi	yi	∆yi	∆²yi	∆³yi
0	1,2	2,0736
			2,8561- 2,0736= 0,7825
1	1,3	2,8561		0,9855-0,7825= 0,2030
			3,8416-2,8561= 0,9855		0,2354-0,2030= 0,0324
2	1,4	3,8416		1,2209-0,9855= 0,2354
			5,0625-3,8416= 1,2209
3	1,5	5,0625

Подставляя полученные значения в начальную формулу получим

P₂(x)= 0,203x² – 1,9858x+ 4,9322.

Убедимся в правильности многочлена P₂(1б3)= 0,203·1.3² – 1,9858·1.3+ 4,9322=2.856.

Тогда P₂(1.25)= 0,203·1.25² – 1,9858·1.25+ 4,9322= 2.7671.

Дата добавления: 2018-02-15; просмотров: 593; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!