Проведя исследование, построить график функции
.
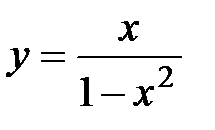Исследование
1. D(y) = (-∞; -1) 
(-1; 1) 
(1; +∞)
2. Непрерывность. Точки разрыва
Как композиция элементарных функций y(x)
является непрерывной в каждом из промежутков
(-∞; -1), (-1; 1) и (1; +∞). Вызывают подозрение точки -1 и 1
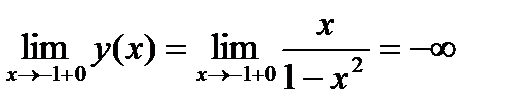
Отсюда следует, что 
не 
и точка
x = -1 – точка разрыва 2-го рода.
3. Функция нечётная, т.к.
Т.к. функция нечётная, то её график симметричен
относительно начала координат.
4. Функция не является периодической.
5. Интервалы знакопостоянства.
а) 
, значит, 
=>y(x)>0 на (-∞; -1) (0; 1)
б) y(x)<0 на (-1; 0) (1; +∞)
в) y(x)=0 в точке x = 0
1. Точки ∩ с осями координат
а) x = 0 =>y = 0
б) y = 0 =>x = 0
Значит, точка (0; 0)принадлежит графику
2. Асимптоты графика
а) Наклонная асимптота: y = kx+b, где
; 
.
=>y = 0 – горизонтальная асимптота.
б) Вертикальная асимптота y = -1, y = 1
3. Исследование с помощью первой производной.
=> критических
точек первого рода нет.
| X | (-∞; -1) | -1 | (-1; 1) | 1 | (1; +∞) |
| y’ | + | - | + | - | + |
| Y | возрастает | - | возрастает | - | возрастает |
4. Исследование с помощью второй производной.
Найдём критические точки второго рода
=>x=0
| X | (-∞; -1) | -1 | (-1; 0) | 0 | (0; 1) | 1 | (1; +∞) |
| y’’ | + | - | - | 0 | + | - | - |
| Y | È | Ç | 0 | È | Ç |
5. Поведение на ∞.
.
Найти решение указанной задачи
Решение
Билет 16
Метрические пространства.Непрерывные функционалы. Св-ва ф-ций, непрер-ых на компакте.
|
|
|
ОПР X-нек мн-во, метрикой на Х наз отображения: 
приним-я неотриц-е зн-я,т что вып-ны аксиомs метрики:1) p(x,y)=0 
x=y 2) p(x,y)=p(y,x) 3) p(x,y)<p(x,z)+p(z,y). Зн-е p(x,y) на паре x,y наз расстоянием м/у x и y.Мн-во X б.наз. пр-вом,а подмн-во пр-ва X мн-ми в пр-ве X.ОПР Мн-во X с заданной на нем метрикой б.наз.метрическим пр-вом и обозн (X,p). Мн-во 
.
Пара 
наз подпр-вом пр-ва (X,p)
Пусть (X,p),(Y,d) метр пр-ва, от-е 
назыв непрер в т.х0, если 
. f назыв непрер в т., если 
назыв компактом, если люб открытое подпокрытие К сод-т кон-е подпокр.
Теор: 
предкомп 
Е равном огранич и равном непрер.
назыв равном непрер, если 
назыв равном непрер, если 
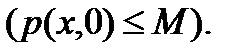
Квадратичные формы (преобразование квадратичной формы при линейном однородном преобразовании переменных; канонический вид квадратичной формы; закон инерции квадратичных форм (индекс инерции квадратичных форм); нормальный вид действительных и комплексных квадратичных форм; положительный и отрицательный индексы инерции действительных квадратичных форм; положительно определенные квадратичные формы).
Пусть Р-поле и 
-перем, тогда мн-н вида 
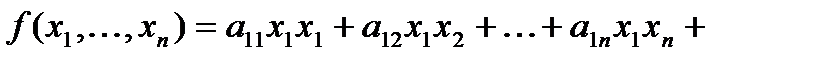
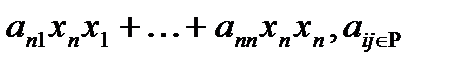-назыв квадрат формой от перем над пол Р.
Сист рав-в 
назыв лин преобраз переем над пол Р.
|
|
|
Квадр форма 
назыв канонич, если фактич она им вид: 
.
Теор: (зак итер кв форм): Число ненул коэф в канонич виде кв формы не завис от выб невыр лин преоб перем, преобр-их исх кв форму в канон вид.
Индексом инерции кв формы наз-ся ненул коэф в каконич виде кв формы.
Норм видом дейст кв формы назыв такой её канонич вид, в кот все ненул коэф есть либо 1 либо -1.
Норм видом компл. Кв формы назыв такой её канонич вид, в кот люб её ненул коэф есть 1.
Теор: Число положит коэф в канонич виде действит кв формы не завис от выб невыр лин преоб-ий перем над R, преобраз-их исх кв форму в дан канонич вид.
Теор: Для люб действит кв формы сущ такое невыражд лин преобр её переем, кот преобр дан форму в норм вид.
Действит кв форма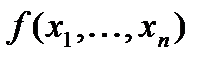 
назыв положи определ, если 
всяк рак, когда одно из чисел 
- ненул. Анал опр отриц определ.
Теор: если из 2-х эквив действит форм одна из явл положи (отриц) опред, то таковой явл и другая из них.
16. Вычислить следующие интегралы:
а) 
б) 
.
а 
б)
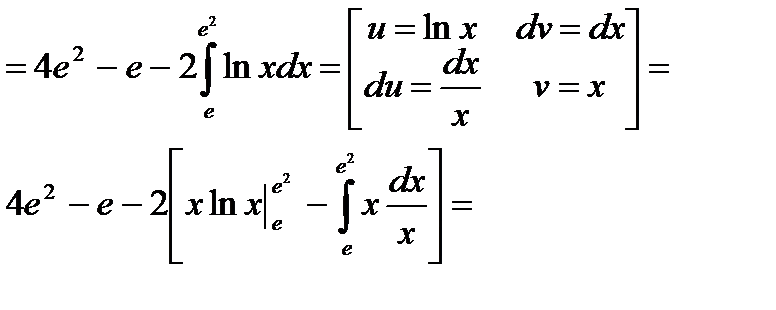
Дата добавления: 2018-02-15; просмотров: 504; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!