Одношаговые методы решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка.
Пусть дана система ДУ 1-го порядка 
(1), с начальными условиями 
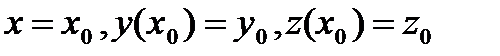(2).
В этом случае получаем:
(3),
где 
,
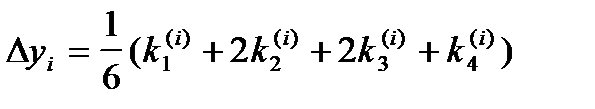(4),
где коэффициенты k, l определяются следующим образом:
;
;
;
;
;
;
;
.
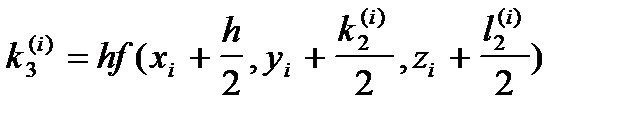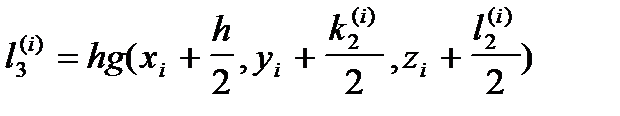И тогда решение в (i+1) точке находится по формуле (3).
Решение систем дифференциальных уравнений методом Адамса.
Пусть задана система 2-х дифференциальных уравнений
y’=f1 (x,y,z)
z’=f2 (x,y,z) (1)
c начальными условиями y(х0)=y0, z(x0)=z0.
Тогда для системы 2-х уравнений решения по экстрополяционной формуле Адамса можно записать в виде:
, 
, 
где 
, 
(3)
Найти площадь фигуры, ограниченной кривыми
y = 2x - x2, x + y = 0.
Решение
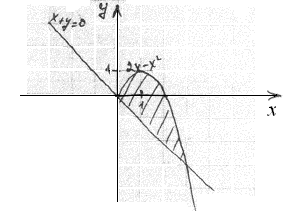
x = 0, x = 3
Ответ: 9/2.
19Найти базис и размерность линейной оболочки 
векторов из 
, где 
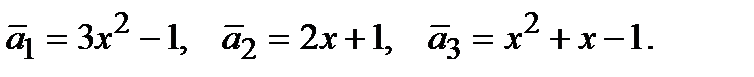
Решение:
Рассмотрим систему векторов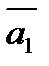 
, 
. И пусть 
θ, θ=0+0х+0х2
Это приводит к системе:
Система имеет единственное решение: 
И поэтому вектора 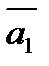, линейно независимы.
Рассмотрим систему векторов , ,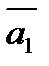 
(1)
Пусть 
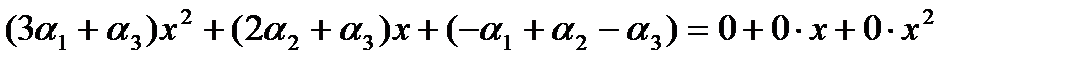
Это приводит к системе: 
Определитель системы ≠ 0 → система имеет единственное нулевое решение. Значит, система векторов (1) является базисом линейной оболочки. LimL(a1, a2, a3)=3
Ответ: базис: 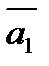, , , LimL(a1, a2, a3)=3
Билет 20
Производная ф-ции комплексного переменного. Аналитичность. Степенной ряд, круг его сходимости. Ряд Тейлора.
|
|
|
Пусть f опред в обл Д, тогда произв в т.z. Пусть f опред в некот окр 
т. 
. Если сущ кон пред 
, то он назыв произв функ f в т. Z0 и об-ся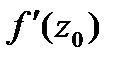 
. Из опред произв и св-в пред получ осн прав диф-я, аналог соотв-м прав диф-го исчисл ф-й действит перем.
Фун f, опред в окр т. 
, назыв аналит-ой в т. 
, если она диф-ма в нек окр этой т. Т.о. множ-во точек аналитичности ф-ии открыто. Ф-я, анал-я в кажд т.откр множ Д, наз аналитич в Д, или голоморфной, моногенной, правильной. Ф-я 
, назыв анал-ой в замкн обл 
, если сущ анал ф-я 
, так, что обл Д1 сод и 
для всех 
. Анал ф-я во всей пл-ти С назыв целой.
-степ ряд. Ему можно пост в соотв рад R и круг с центр в т. рад R, U(z0,R) – круг сход-ти. R-рад сх-ти, U(0,R) –круг сх-ти.
Теор: Если ф-я f анал-я, то в окр произ т. 
, 
ф-я 
, причём R ряда не меньше, чем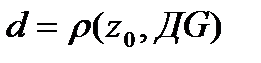 
, а коэф 
, где 
=окр с центр в т. , 
. Ряд назыв рядом Тейлора.
Симплекс-метод (критерий оптимальности, алгоритм).
Основной метод ЛП - СМ, разработанный для специальной задачи в канонической форме:
c'x→max, Ax=b, x≥0. (1)
ЦФ - maxимизируется, а все переменные имеют ограничения.
Введем обозначения:
J={1,…,n} - множество индексов переменной xj.
I= {1,…,m} - множество #-ов основных ограничений.
aj= 
Є Rm- j-ый столбец матрицы А. Вектор х Є Rm - базисный план (1), . если он удовлетворяет всем ограничениям задачи, и его переменные разбиты на 2 группы: 1. базисные: xj1,… xjm.; и 2. не базисные xj, j Є Jh=J\JБ. Причем: 1. xj=0, j Є Jh.; 2. aj, jЄJБ - линейно независимы в Rm. 3. Если составить матрицу АБ= (aj, jЄJБ), то det АБ≠0. Эта матрица называется базисной.
|
|
|
Критерий оптимальности: Пусть известен БП (xj, JБ), тогда: ∆н≥0 - достаточно, а для невыражденного БП необходимо для его оптимальности.
Достаточно: пусть ∆н= хн - хн ≥0., хн ≥0, хн =0. Тогда: с'х - c'x, для всех х ЄХ, х - оптимум.
Необ-мо: Пусть х -ОБ и невырожденный план → хБ>0.
Предположим противное, т.е. существует j0ЄJн: ∆j0<0.
Построим вектор приращений ∆х с.о.: пусть ∆хj=0, j Є Jh\r0, а ∆хj0= Θ≥0.
Базисные компоненты приращений подбирают т.о. что бы оставалось А∆х=0 и ∆хБ= -А-1БАн∆хн.
При выполнении этих условий вектор ∆х будет удовлетворять основным ограничениям задачи (1). →∆хБ= - ΘА-1БАнaj0. Построим вектор хн = х+∆х.
Θ можно подобрать т.о., ч.б. вектор х был планом задачи, т.е. х>0.
Тогда, план х лучше х, т.е. получаем противоречие с оптимальностью х.
Алгоритм:
Пусть имеется объект, поведение которого надо оптимизировать.
1.изучение и описательное регулирование.
а) изучение структуры объекта.
|
|
|
б) изучение основных способов функционирования составных частей.
в) выясняют цель оптимизации.
г) собирают конкретную цифровую информацию о структуре функции и цели объекта.
2. Мат-кое моделирование.
а) построение неизвестных параметров х1,…,хn, которые однозначно описывают поведение объекта изменением которых можно выполнить достижение цели.
б) запись основных связей и закономерностей функционирования объекта с помощью введенных неизвестных хjи мат. операций. В результате приходим к системе ограничений на хj. В совокупности все эти ограничения и задают множество планов Х, а именно: вектор х т.т.т. является планом, если он удовлетворяет всем ограничениям одновременно.
в) запись с помощью неизвестных и мат. операций ЦФ f(x).
После чего, мы приходим к задаче в форме (1).
3. Теоретическое исследование и выбор метода, вкл. в себя:
а) выяснение к какому классу задач оптимизации относится наша.
б) изучении теории по данному классу задач и методах которые для него имеются. Если нет, то работают доп. исследования, учитывающие специфику задачи. Модифицируется или разрабатывается новый метод.
4. Построение ОП.
а) выясняем им-ся ли программа реализации нашего метода: Да- то используем; Нет- строим свою.
|
|
|
б) вводим в программу числовые параметры конкретной задачи.
5. Исследование. Сравнивается полученный ОП с реальным поведением объекта. Если есть возможность, то проводим эксперимент.
Если решение нас не удовлетворяет, то процесс решения задачи оптимизации может быть улучшен на всех этапах 1-4. При решении задачи оптимизации, возможны ошибки погрешности во всех 5 пунктах.
Дата добавления: 2018-02-15; просмотров: 590; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!