Касательные напряжения при изгибе
Выше говорилось, что в общем случае поперечного изгиба в сечениях балки, кроме изгибающего момента, возникают поперечные силы, то есть балка помимо изгиба испытывает срез и, соответственно, возникают касательные напряжения.
В силу закона парности касательных напряжений они возникают не только в плоскостях сечений, но и в продольных плоскостях, параллельных нейтральному слою. Они имеют одинаковую величину в каждой точке сечения, но в различных точках они различны, то есть распределение касательных напряжений по высоте сечения неравномерно.
Закон распределения касательных напряжений по высоте сечений различен для различных их форм. Наиболее характерно прямоугольное поперечное сечение, где этот закон устанавливается достаточно просто.
Вырежем в зоне обычного поперечного изгиба (см. рис. 9.1) бесконечно близко расположенными плоскостями 1-2 и 3-4 в балке прямоугольного поперечного сечения элемент длиной dx (рис. 10.2). Далее вывод формул касательных напряжений ведут в следующем порядке.
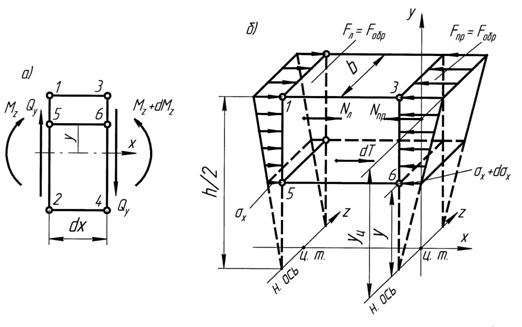
Рис. 10.2 К выводу формулы касательных напряжений при изгибе
1. Элемент 1-2 – 3-4, находясь в составе балки, был в равновесии, по грани 1-2 действовали внутренние усилия 
и 
, а по грани 3-4 - и 
(см. рис. 10.2, а).
2. Мысленно срежем в рассматриваемом элементе его верхнюю часть. Нижняя грань этой срезанной части параллельна нейтральному слою (элемент 1-5-3-6 на рис. 10.2, б) и удалена от него на ординату у.
|
|
|
3. Просуммируем элементарные продольные силы, действующие на левую 
и правую 
грани этого элемента, причем очевидно, что 
, где 
- площадь отсеченной части поперечного сечения (площадь обреза).
;
.
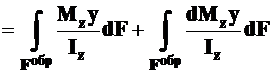Теперь обратим внимание на то, что, если бы вдоль балки не существовало касательных сил, то произошел бы сдвиг элемента 1-5-3-6 справа налево, но этого не происходит, значит должна существовать какая-то касательная сила 
, действующая в плоскости обреза и уравновешивающая силы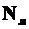 
и 
.
4. Спроектируем все силы на ось Х
; 
,
откуда
(1П)
В формуле (1) 
- статистический момент части поперечного сечения, расположенный выше уровня У, то есть осеченной его части относительно оси Z.
5. Полагаем, что элементарная касательная сила dT не меняется по длине элемента dx, тогда интенсивность этих сил на единицу длина будет равна
, (2П)
где 
- по теореме Журавского (см. формулу 8.2) поперечная сила в сечении, совпадающем с осью У.
Формула (2П) дает закон распределения касательных срезывающих сил по высоте сечения, так как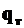 
пропорциональна 
- статистическому моменту отсеченной части сечения, но не напряжений. Она справедлива при любой форме профиля, если только соблюдено условие о взаимной перпендикулярности нейтральной оси Z и силовой линии У.
|
|
|
Анализ формулы (2) показывает:
1. Интенсивность касательных сил пропорциональна и меняется по высоте балки по тому же закону, что и статистический момент 
, то есть касательные силы достигают максимума в нейтральном слое.
2. Изменение интенсивности касательных сил по высоте балки вызывает изменение углов сдвига и, следовательно, искажение плоскости поперечного сечения, поэтому вывод формулы нормальных напряжений сделан для чистого изгиба.
3. Для перехода от интенсивности касательных сил к касательным напряжения необходимо знать, как распределяются эти силы по ширине сечения. Элементарное решение задачи существует только для прямоугольного профиля, при котором распределение касательных сил по ширине сечения можно считать равномерным (при 
> 
). В этом случае
(10.13)
Выражение (10.13) носит название формулы Д.И. Журавского. Необходимо помнить, что, хотя все приведенные выше рассуждения относились к касательным силам и напряжениям, действующим в плоскостях, параллельных нейтральному слою, они, в соответствии с законом парности касательных напряжений, автоматически относятся и к касательным напряжениям, действующим в поперечном сечении.
|
|
|
Найдем развернутое выражение касательных напряжения для прямоугольного сечения (рис. 10.3).
Рис. 10.3 К выводу формулы максимальных касательных напряжений
при изгибе
В соответствии с рис. 10.3
,
то есть статистический момент отсеченной части сечения меняется по закону параболы. Тогда
,
то есть и касательные напряжения меняются по высоте сечения по закону параболы (см. эпюру 
на рис. 10.3). Максимальные касательные напряжения будут в нейтральном слое, то есть при 
, (10.14)
где F – площадь поперечного сечения.
Лекция 11
Дата добавления: 2018-02-15; просмотров: 529; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!